曲率（読み）キョクリツ（その他表記）curvature

デジタル大辞泉

きょく‐りつ【曲率】

曲線や曲面の曲がりの度合いを示す値。曲線上の近い二点のそれぞれの接線がつくる角と、二点間の弧の長さとの比の極限値で表す。曲率が大きいほど湾曲は大きく、また円では一定である。

出典　小学館

精選版 日本国語大辞典

きょく‐りつ【曲率】

1. 〘 名詞 〙 曲線、曲面の曲がりの度合。曲線上の点Ｐのごく近くに点Ｑをとり、ＱをＰへ限りなく近づけたときの、点Ｑにおける接線のなす角と二点の間の弧の長さの比の極限値κによって表わす。〔工学字彙（1886）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

曲率 (きょくりつ)
curvature

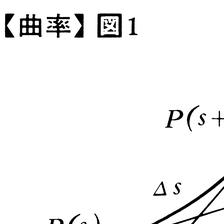
曲線や曲面の曲がる度合を表す量をいう。まず，平面上の曲線の場合を考えよう。曲線Cを弧長sを用いて媒介変数表示し，弧長sの点をP（s）で表す。また，Cの各接線には曲線の正の向き（sが増すときにP（s）の動く向き）と同じ向きをつける。いま，sを固定して，P（s）における接線の向きからPの近くの点P（s＋⊿s）における接線の向きまでの回転角を⊿θ（ラジアン）とし，比⊿θ/⊿sを考える（図1）。⊿sを0に近づけたときのこの比の極限をPにおけるCの曲率という。これをkで表すとき，ρ＝1/｜k｜を曲率半径という。kの正負に応じて，sが増すときPの近くでCは左または右に曲がり，その曲がり方はρが大きいほどゆるやかである（図2）。Pとこれに近いC上の2点Q，Rを通る円の，Q，RをCに沿ってPに近づけたときの極限の円をPにおけるCの接触円osculating circleという。これはPにおけるCの接線にPで接し，その接線に関してCと同じ側にあり，ρを半径とする円である（図2）。このようなわけで，接触円をまた曲率円と呼び，その中心を曲率中心center of curvatureという。空間内にある曲線に対しても，曲率が同様に定義される。ただし，空間においては2直線の向きの間の回転角に符号がつけられないので，曲率の定義における⊿θはP（s）とP（s＋⊿s）における接線のなす角に⊿sと同じ符号をつけたものとする。したがって空間曲線ではk≧0となる。接触円の定義は空間曲線に対しても意味をもち，その半径は曲率の逆数となる。次に，曲面の場合を考えよう。図3においてSを曲面とし，Pをその上の1点とする。PにおけるSの法線（PにおいてSに垂直に交わる直線）を含むすべての平面を考え，これらの平面によるSの切口である曲線の曲率（≧0）に，法線のある向きに関して曲線が凹であるか凸であるかに応じて正負の符号をつける。これらの最大値および最小値をPにおけるSの主曲率といい，これらの相加平均を平均曲率，これらの積をガウス曲率または全曲率という。全曲率が正ならば，Pの近くの点は接平面の片側にあり，全曲率が負ならばPの近くで曲面は馬の鞍（くら）の形をしている。曲面上のすべての点において全曲率が0のとき，この曲面は平面上に伸縮なしにひろげることができる。
執筆者：中岡 稔

図1～図3

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

曲率
きょくりつ

曲線の曲がっている度合いを表す数。曲線上の隣接3点を通る円の半径、すなわち曲率半径の逆数として定められる。直線は曲率ゼロであり、曲線は曲率が大きいほど曲がり方が大きい。

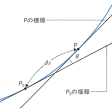
　平面上の曲線y=f(x)に対して、f(x)が2回微分可能であるとするとき、この曲線上の点P0(x0,y0)と曲線上の隣接する2点を通る円（曲線上にP₀と異なる点P₁、P₂をとり、P₀、P₁、P₂を通る円をつくって、P₁、P₂をP₀に近づけたときの極限の円）をP₀における曲率円という。その半径の逆数が曲率で、それは、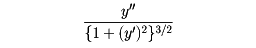

となる。この値はy″の正負によって正、または負となるが、曲率が正とはxが増加するとき曲線が左側（すなわち正の方向）に曲がっていくこと、負とは右側に曲がっていくことを意味する。

　曲率は、また、P₀とその近くの点Pとにおける接線のなす角をθ、P₀とPの間の曲線の弧の長さをΔsとして、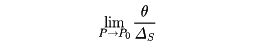

という式で与えることもできる。曲率は曲線の形状を特徴づける数である。空間曲線や、曲面の曲率も定義される。さらにリーマン幾何学においては空間の曲率も定義される。

［竹之内脩］

曲率説明図

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

曲率【きょくりつ】

曲線または曲面の曲がる度合を表す量。（１）平面曲線上の一点Pから近くの点Qまでの曲線の弧の長さをΔsとし，Pにおける曲線の接線とQにおける曲線の接線がなす角をΔθ（ラジアン）とするとき，QがPに無限に近づいたとき比Δθ/Δsがとる極限値を曲率という。これをκで表すとき，ρ＝1/｜κ｜を曲率半径といい，曲線の曲がり方はρが大きいほどゆるやかである。点Pでこの曲線に接する円で，半径が曲率半径に等しく，共通接線に関し曲線と同側にあるものを，点Pにおけるこの曲線の曲率円といい，その中心を曲率中心という。同様に空間内の曲線についても曲率を定義できるが，２接線のなす角に符号がつけられないので，｜Δθ/Δs｜として考える。（２）曲面ではその上の１点Pにおける曲率として考える。法線を含む平面で曲面を切り，切口の曲線の点Pにおける曲率半径をRとする。平面の向きをいろいろに変えれば，Rも変化し，最大値R₁と最小値R₂をとる。1/R₁，1/R₂を主曲率，（1/R₁＋1/R₂）/2を平均曲率，1/R₁R₂を全曲率またはガウスの曲率という。
→関連項目クロソイド｜縮閉線

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

曲率
きょくりつ
curvature

曲線および曲面について定義される。 (1) 曲線の曲率　曲線上の点Pが曲線に沿って動くとき，その進行方向は，移動した距離 (曲線の弧長) s に伴って変化する。このときの変化率を曲線の曲率という。いま平面曲線上の定点PからQまでの微小な移動距離を Δs ，その2点P，Qにおける2つの接線がつくる角 ( s の増加方向の) を Δθ とすれば，方向の変化率 κ は，Δs が0に近づくときの Δs/Δθ の極限で与えられる。これをこの曲線の点Pにおける曲率という。 κ の逆数 ρ＝1/κ を曲率半径という。これは接触円の半径になる。空間曲線についても同様である。 (2) 曲面の曲率　これには，法曲率，測地的曲率，全曲率 (ガウスの曲率) ，平均曲率がある。

出典　ブリタニカ国際大百科事典 小項目事典