角速度（読み）カクソクド

デジタル大辞泉

かく‐そくど【角速度】

物体が回転運動をするときの回転の速さを、単位時間の回転角で表したもの。単位はラジアン毎秒。

出典　小学館

精選版 日本国語大辞典

かく‐そくど【角速度】

1. 〘 名詞 〙 物体がある軸のまわりを回転する速さを表わす量。回転軸に垂直に引いた、物体に固定した垂線の方向の、時間的な角度変化の割合をいう。反時計方向を正、時計と同じ方向を負とするのが普通。単位、ラジアン毎秒。〔工学字彙（1886）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

角速度
かくそくど

質点または剛体の瞬間的な角回転の割合として定義される速度。すなわち、平面上を運動する点と原点を結ぶ直線が、微小時間dt中に原点の周りに角度dθだけ変化したとき、dθ/dtが運動点の原点の周りの角速度の大きさである（図）。原点を通り回転面に垂直な軸方向で、かつ回転によって右ねじの進む向きを正とする単位ベクトルをnとする。そのときω＝nωを大きさωの角速度ベクトルあるいは単に角速度という。

　角速度ωのとき原点Oから位置ベクトルrにおける速度vはベクトル積ω×rで与えられる。すなわち、ある瞬間においてP点の運動は、Pから回転軸へ下ろした垂線の長さρ＝rsin（はOPと回転軸のなす角）を半径とし、垂線の足Qを中心とする円運動であるから、速度vの大きさはv＝ωrsinである。方向はωとrに垂直で、向きはωからrへ右ねじの進む向きで、vはω×rに等しい。運動点の描く曲線上の点において、加速度は接線および法線方向にdv/dt、v²/ρの成分をもつ。前者を接線加速度、後者を法線加速度とよぶ。速度ベクトルvは、空間曲線に沿っての長さをsとすれば、大きさはds/dtで、向きは接線方向、ρは軌道の曲率半径ds/dθである。接線加速度は速度の大きさの時間的変化であって方向の変化には関係ない。また法線加速度は速度の大きさの変化には関係なく速度自身と軌道の形に依存する。接線加速度がゼロの場合は、加速度は速度すなわち軌道に垂直になる。角速度ωとの関係は、速度がρωだから法線加速度はρω²である。これを向心加速度ともいう。遠心力はこの加速度と反対の向きに働く。

［村岡光男］

[参照項目] | 回転運動

角速度〔図〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

角速度 (かくそくど)
angular velocity

一平面（xy面とする）上を運動する点Pがあるとき，原点OとPを結ぶ線分OP（動径という）とx軸の間の角θは時間tとともに変化する。このときdθ/dtをP点がOまたはz軸に対してもつ角速度という。半径Rの円周上を速さVで動く点が円の中心に対してもつ角速度ωはω＝V/Rである。広がりをもつ物体の回転運動は，各瞬間の回転軸とそのまわりの角速度の大きさωで与えられるが，これを大きさがωで，回転軸の回転方向に右ねじを回したとき右ねじの進む向きを方向とするベクトルで表すことが可能で，これを角速度ベクトルという。速度ベクトルと異なり，角速度ベクトルは，なにかある時間変化するベクトルを時間で微分したものとして表すことは一般には不可能である。質量と速度の積が運動量となるのに対応して，慣性モーメントと角速度の積が角運動量を与える。
執筆者：小出 昭一郎

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

角速度
かくそくど
angular velocity

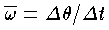物体がある直線のまわりを回転する速さの程度を表わす量。この直線を回転軸という。回転軸に垂直な直線が物体とともに，時間 Δt の間に角 Δθ だけ回転するとき， を平均角速度といい，Δt がゼロに近づくときの 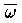の極限値を瞬間角速度または単に角速度といい，ω で表わす。
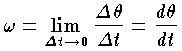角速度をベクトルと考えると便利なことがある。角速度ベクトル ω は ω を大きさに，回転軸に沿って回転の向きに回した右ねじの進行方向を向きにもつ (図参照) 。物体が固定点O を通る軸のまわりに角速度 ω で回転運動するとき，点O に関し位置ベクトル r をもつ物体上の点の回転に伴う速度は v＝ω×r である。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

角速度【かくそくど】

平面上を運動する点と原点を結ぶ線分（動径）が，原点を通る定直線（基線）となす角が，時間的に変化する割合。原点を通り平面に垂直で，基線からこの動径の方向へまわした右ねじの進む向きのベクトルで表される。国際単位はラジアン/秒。角速度の時間的変化の割合は角加速度という。→角運動量／角運動量保存の法則
→関連項目円運動｜慣性モーメント｜向心力｜速度

出典　株式会社平凡社

栄養・生化学辞典

角速度

　ある原点と運動する物体を結ぶ直線を引き，原点を通る一定の線Aとの間の角度をxとするとき，dx/dt．

出典　朝倉書店