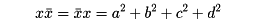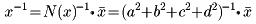四元数 (しげんすう)
quaternion
複素数の一つの拡張として,W.R.ハミルトンによって考えだされた数である。四元数αは2乗して-1になる三つの数i,j,kによって,
α=a+bi+cj+dk (a, b, c, dは実数)
と表され,二つの四元数α,α′(=a′+b′i+c′j+d′k)の和は,
α+α′=(a+a′)+(b+b′)i+(c+c′)j+(d+d′)k
で定められる。二つの四元数の積は,
ij=-ji=k,jk=-kj=i,
ki=-ik=j
を用いて定められる。四元数においては四則演算はできるが,ij=-jiのように乗法の交換法則は成り立たない。
複素数と同様に,αに対し,その共役ᾱをᾱ=a-bi-cj-dkで定めれば,
αᾱ=a2+b2+c2+d2
となり,α≠0ならばαᾱ≠0である。x=bi+cj+dkの形の四元数全体をVで表し,これを距離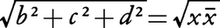 をもつ三次元ユークリッド空間と思うと,Vでの回転は四元数の乗法を用いて,ある四元数αにより,
をもつ三次元ユークリッド空間と思うと,Vでの回転は四元数の乗法を用いて,ある四元数αにより,
x α⁻1xα x∈V
α⁻1xα x∈V
で与えられる。
執筆者:斎藤 裕
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
四元数
しげんすう
quaternion
四つの元1、i、j、kを基底とする実数体R上の線形空間Hを、1を乗法についての単位元とし、
(1)i2=j2=k2=-1
(2)ij=-ji=k, jk=-kj=i, ki=-ik=j
(3)a(xy)=(ax)y=x(ay) (a∈R, x, y∈H)を満たすように乗法を定義することにより、乗法について可換でない体にすることができる。このHを四元数体といい、Hの元
(4)x=a1+bi+cj+dk (a, b, c, d∈R)を四元数という。とくに、(4)でb=c=d=0のような四元数xは実数aであり、c=d=0のようなxは複素数a+biである。この意味で、四元数体Hは実数体Rと複素数体Cを部分体として含んでいる。実際、R上有限次線形空間になっている(かならずしも乗法が可換でない)体はR、C、Hに限ることが知られている。
(4)の四元数xに対し、四元数a1-bi-cj-dkを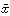 と書き、xの共役四元数といい、
と書き、xの共役四元数といい、
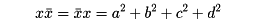
なる実数をN(x)と書き、xのノルムという。
x=0⇔N(x)=0
が成り立ち、x≠0なら、xの逆元は
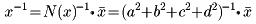
四元数はイギリスの数学者ハミルトンによって1843年に発見されたので、ハミルトンの四元数ともいう。この発見が多元数論の出発点になった。
[菅野恒雄]
出典 小学館 日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について 情報 | 凡例
Sponserd by 
四元数【しげんすう】
複素数を拡張したもので四つの単位1,i,j,kをもち,a,b,c,dを実数としてa+bi+cj+dkの形で表される。二つの四元数の加減は複素数の場合と同様だが積についてはi2=j2=k2=−1,ij=−ji=k,jk=−kj=i,ki=−ik=jとなる。これにより四元数は乗法の交換法則を除くすべての代数法則(結合法則,分配法則)が成り立ち,その集合は非可換体となる。1840年ごろW.R.ハミルトンが発見。幾何学,物理学等に応用される。→数
→関連項目代数学
出典 株式会社平凡社百科事典マイペディアについて 情報
Sponserd by 
四元数
しげんすう
algebra of quaternion
4つの底1,i ,j ,k を i2=j2=k2=-1 ,ij=-ji=k ,jk=-kj=i ,ki=-ik=j を満たすようにとるとき,実数 x0 ,x1 ,x2 ,x3 を係数として,x=x0+x1i+x2j+x3k と表わされる数を四元数という。 1854年,W.R.ハミルトンにより,複素数体の拡張として導入された。四元数は体をつくり,四元数体と呼ばれている。乗法の交換法則は成り立たないので,非可換体である。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
世界大百科事典(旧版)内の四元数の言及
【ピタゴラス】より
…〈万物の原理は数である〉と彼がいうとき,世界は量的関数関係から成り立つ数学的秩序をもっているといったのではなく,万物は数の存在分節機能によって秩序立てられ,存在の各層には同一の数の類比関係が働いているということを意味した。このことを象徴的に表しているのが図に示すような〈四元数(テトラクテュス)〉である。この1,2,3,4から成る10個の点は,大宇宙と小宇宙に共通する世界秩序(コスモス)を表す曼荼羅(まんだら)となっており,ピタゴラス教団ではこの図形の前で誓いを立てたと伝えられている。…
※「四元数」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
Sponserd by 
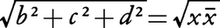 をもつ三次元ユークリッド空間と思うと,Vでの回転は四元数の乗法を用いて,ある四元数αにより,
をもつ三次元ユークリッド空間と思うと,Vでの回転は四元数の乗法を用いて,ある四元数αにより, α⁻1xα x∈V
α⁻1xα x∈V

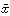 と書き、xの共役四元数といい、
と書き、xの共役四元数といい、