多元環（読み）たげんかん（その他表記）algebra

改訂新版　世界大百科事典

多元環 (たげんかん)
algebra

実数を係数とする二次の正方行列全体をAで，また実数全体をKで表すと，次の（1）（2）が成り立っている。

（1）AはK上の加群である。すなわち，Aの二つの元の和が定義されていて，それについてAはアーベル群（可換群）であり，Kの元λとAの元aの積λa（スカラー倍）が定まっていて次の（a）～（c）の性質をもつ。

　（a）λ（a＋b）＝λa＋λb

　（b）λ₁（λ₂a）＝（λ₁λ₂）a

　（c）1・a＝a

（2）Aの二つの元a，bの積abが定義されていて，（a）～（d）の性質をもつ。

　（a）（ab）c＝a（bc）　　…（結合法則）

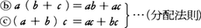
　（d）λ∈K，a，b∈Aのとき，λ（ab）＝（λa）・b＝a（λb）

n次の正方行列全体についても，（1）（2）が成り立っている。一般に集合Aと単位元をもつ可換環Kがあって，上の（1）（2）を満たすとき，Aを環K上の多元環という。実数係数のn次正方行列の全体，四元数全体（Kはいずれも実数全体）は多元環のたいせつな例である。これ以外にも数学においては多くの多元環が現れ，重要な研究対象になっている。以下，多元環の例をいくつかあげよう。

例1

外積代数　Vが実数全体のなす体K上の三次元ベクトル空間であり，e₁，e₂，e₃がその1組の基底であるとする。∧（V）が1，e₁，e₂，e₃，e₁∧e₂，e₂∧e₃，e₃∧e₁，e₁∧e₂∧e₃を基底とするベクトル空間であるとし，積∧（外積）は性質，

　e_i∧e_i＝0　e_i∧e_j＝－e_j∧e_i　（i≠j）

で定められるものとする。例えば，

　（e₁∧e₃）∧e₁＝－（e₃∧e₁）∧e₁＝－e₃∧（e₁∧e₁）＝0

　（ae₁＋b（e₁∧e₃））∧（e₃∧e₂）＝ae₁∧（e₃∧e₂）＋b（e₁∧e₃）∧（e₃∧e₂）

　　＝－ae₁∧e₂∧e₃

である。∧（V）は積∧をもつ多元環である。これを外積代数，またはグラスマン代数Grassman algebraという。一般のベクトル空間に対しても外積代数が考えられる。

例2

群環　Gが有限群で，Kが体であるとき，Gの元のK上の一次結合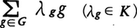の全体をK［G］で表し，K［G］の乗法をGの演算によって定めればK［G］はK上の多元環となる。これをGのK上の群多元環，あるいは群環という。

例3

実数全体で連続な関数で，ある有界集合の外では0になるもの全体をCで表し，Cの元f，gの積を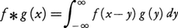，で定めれば，Cは実数全体のなす体上の無限次元の多元環となる。また，積に関する結合法則（2）の（a）を満たさない多元環を考えることもある。
執筆者：斎藤 裕

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

多元環
たげんかん
hypercomplex system; algebra

線形環ともいう。訳さずにアルジェブラということもある。単位元をもつ環を R ，アーベル群を G とし，演算としては，G 内の加法以外に，R の元と G の元との間に乗法が定義されているものとする。このとき G が，
(1) a∈R ，v∈G に対して av∈G
(2) a∈R ，v₁，v₂∈G に対して
　 a(v₁＋v₂)＝av₁＋av₂
(3) a₁，a₂∈R ，v∈G に対して
　 (a₁＋a₂)v＝a₁v＋a₂v
(4) a₁，a₂∈R ，v∈G に対して
　 (a₁a₂)v＝a₁(a₂v)
という4条件を満たせば G は線形加群 (ベクトル空間) となる。ここでさらに任意の元 v₁，v₂，v₃∈G に対して，条件
(5) 結合法則 (v₁v₂)v₃＝v₁(v₂v₃)
(6) 分配法則 v₁(v₂＋v₃)＝v₁v₂＋v₁v₃
　 (v₂＋v₃)v₁＝v₂v₁＋v₃v₁
(7) a∈R ，v₁，v₂∈G に対して
　 (av₁)v₂＝v₁(av₂)
を満足するような乗法を定義することができれば，G は環になる。この環 G のことを，環 R の上の多元環という。 R の代りに体をとることも多いが，必ずしも体である必要はない。多元環の元のことを多元数という。

出典　ブリタニカ国際大百科事典 小項目事典

日本大百科全書(ニッポニカ)

多元環
たげんかん

環Rがあり、それが可換体k上の有限次元のベクトル空間にもなっていて
　　（＊）　λ∈k,a,b∈R
のとき
　　λ(ab)=(λa)b
が成り立つとき、Rを可換体k上の多元環という。手近な例としては、実数体k上の二次の行列全体M₂を考えるとよい。M₂は環であり、一方、実数λを行列Aに掛けることも定義されている。M₂は実数体上の四次元のベクトル空間であり、特性（＊）も成り立っている。実数体k上のn次の行列全体M_nも同様である。また別の手近な例としては、複素数の全体Cを考えればよい。Cは実数体k上の二次元ベクトル空間である。二次の行列全体M₂の場合には、M₂は体ではないが、複素数の全体は体である。

　多元環が体であるとき、多元体とよばれる。多元体として有名な例はハミルトンの四元数体である。複素数を記号iにi²=-1という演算を設けてa+bi（a、bは実数）と表される数として定義したように、記号i、j、kに
　　i²=j²=k²=-1, ij=-ji=k,
　　　jk=-kj=i, ki=-ik=j
という演算を設け
　　a+bi+cj+dk （a,b,c,dは実数）
と表される数を定義する。これをハミルトンの四元数という。ハミルトンの四元数の全体は実数体k上の四次元の多元体である。複素数が実数を拡張した新しい数であるように、ハミルトンの四元数は複素数をさらに拡張した新しい数である。しかし乗法は非可換であることに注目したい。それでは、この四元数をさらに拡張して、多元体をつくることはできないか。興味あることに、もはやそれはできない。すなわち「実数体上の（有限次元の）多元体は、実数体、複素数体、四元数体に限ること」が証明されている。

［寺田文行］

[参照項目] | 環 | 四元数

出典　小学館　日本大百科全書(ニッポニカ)