翻訳|normal
精選版 日本国語大辞典 「法線」の意味・読み・例文・類語
ほう‐せんハフ‥【法線】
日本大百科全書(ニッポニカ) 「法線」の意味・わかりやすい解説
法線
ほうせん
normal
平面上で曲線上の点P0において、その点における接線に直交する直線を、その点における曲線の法線という。曲線がy=f(x)の形で与えられているとき、この上の点P0(x0,y0)における接線の方程式はy-y0=f′(x0)(x-x0)であるから、法線の方程式はx-x0+f′(x0)(y-y0)=0となる。
[竹之内脩]
改訂新版 世界大百科事典 「法線」の意味・わかりやすい解説
法線 (ほうせん)
normal
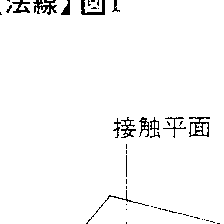
曲線C上の1点PにおいてCに接線tが引けるとき,Pを通りtに垂直な直線をPにおけるCの法線という。Cが平面曲線のときPにおけるCの法線はただ一つであるが,空間曲線のときはそれは無数に存在して,それらの全体はtに垂直な平面をつくる。この平面をPにおけるCの法平面という。空間曲線に対しては,点Pにおける接触平面上にある法線を主法線といい,接触平面に垂直な法線を従法線,または陪法線という(図1)。曲面S上の1点PにおいてSに接平面がつくれるとき,Pを通りこの接平面に垂直な直線をPにおけるSの法線という(図2)。
執筆者:中岡 稔
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
百科事典マイペディア 「法線」の意味・わかりやすい解説
法線【ほうせん】
出典 株式会社平凡社百科事典マイペディアについて 情報
ブリタニカ国際大百科事典 小項目事典 「法線」の意味・わかりやすい解説
法線
ほうせん
normal
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
世界大百科事典(旧版)内の法線の言及
【接平面】より
…この平面を点Pにおける曲面Sの接平面と呼び,Pをその接点と呼ぶ。なお,Pにおいて接平面に立てた垂線を点Pにおける曲面Sの法線という(図1)。点Pが中心をOにもつ球面上にあるとき,Pにおける接平面はPを通り半径OPに垂直な平面である。…
※「法線」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...