精選版 日本国語大辞典 「虚数」の意味・読み・例文・類語
きょ‐すう【虚数】
改訂新版 世界大百科事典 「虚数」の意味・わかりやすい解説
虚数 (きょすう)
imaginary number
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
日本大百科全書(ニッポニカ) 「虚数」の意味・わかりやすい解説
虚数
きょすう
実数の範囲では負の数の平方根は求められない。たとえば、二次方程式x2=-1は、実数の範囲では解くことができない。そこで、2乗すれば-1になる数を考えて、それをiという記号で表す。すなわち、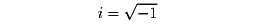
となる新しい数を導入すれば、すべての二次方程式を解くことができる。このiを虚数単位とよび、a、bを任意の実数としてa+biの形に表される数を複素数という。ここで、b≠0である複素数を虚数imaginary number(想像上の数)といい、とくにa=0, b≠0である複素数biを純虚数という。実数real numberは、複素数a+biのb=0の場合をさしていい、したがって、実数は複素数のなかに含まれる。
[寺田文行]
ブリタニカ国際大百科事典 小項目事典 「虚数」の意味・わかりやすい解説
虚数
きょすう
imaginary number
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「虚数」の意味・わかりやすい解説
出典 株式会社平凡社百科事典マイペディアについて 情報
デジタル大辞泉プラス 「虚数」の解説
世界大百科事典(旧版)内の虚数の言及
【数】より
…16世紀になってヨーロッパの数学が急速な発達を始め,17世紀になってG.ライプニッツらにより無限や連続が意識されるようになり,19世紀になって,A.L.コーシー,J.W.デデキント,G.カントルらによって実数概念が確立されたのであり,これは解析学の発展と密接な関連がある。他方,三次方程式の解法に関連して,G.カルダーノが負の数の平方根を利用したのが虚数の導入の最初であるが,数として導入したのでなく,計算の補助手段としての利用であった。虚数と実数を併せたものを数として扱うようになったのは18世紀末ころからであり,先駆的人物がL.オイラー,最重要人物がC.F.ガウスである。…
※「虚数」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...


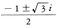 は虚数であってx3=1の根であることから1の虚立方根と呼ばれる。f(x)が実係数の多項式のときには,虚数α=a+biがf(x)=0の根ならばαの
は虚数であってx3=1の根であることから1の虚立方根と呼ばれる。f(x)が実係数の多項式のときには,虚数α=a+biがf(x)=0の根ならばαの