改訂新版 世界大百科事典 「解析接続」の意味・わかりやすい解説
解析接続 (かいせきせつぞく)
analytic continuation
複素平面の領域D1で定義された正則関数f1と,D2で定義された正則関数f2があり,D1∩D2≠φであって,しかもD1∩D2の各点でf1とf2の値が一致するとする。このときf2はf1のD2への解析接続という。この定義をするのみならば,f1やf2の正則性は必要ないが,正則性があるときには次の著しい性質がある。すなわち,一致の定理によって,解析接続は存在すればただ一つに限る。
解析接続を行う方法には,いろいろある。例えば,中心がa,半径がr1の円板D1で正則なf1を,点b∈D1でべき級数に展開したとき,もし収束半径r2がr1-|a-b|より大きいならば,fはD2={z|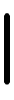 z-b
z-b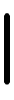 <r2}に解析接続されたことになる。
<r2}に解析接続されたことになる。
Dで定義された正則関数が,Dより広い領域に解析接続することが不可能なとき,Dの境界をfの自然境界という。任意のDに対しこのようなfはつねに存在することが知られている。
上述の解析接続を直接接続ともいい,それを2回以上行うことを間接接続と呼ぶ。例えば,k=1,2,……,nに対して領域Dkで定義された正則関数fkがあり,fk+1はfkのDk+1への解析接続となっているとき,これを解析接続の鎖といい,fnをf1のこの鎖による間接接続という。
曲線C:[0,1]∋t→z(t)において,tごとに,z(t)を含む領域Dtとそこにおける正則関数ftが与えられており,各tに対してδ>0が存在し,|t-t′|<δであるようなすべてのt′に対するft′はftのDt′への解析接続になっているとき,これを曲線Cに沿う解析接続という。f1はf0の,曲線Cによる間接接続という。
本質的には,鎖によるものと曲線によるものとの間には相違はない。
直接接続でも,間接接続でも,得られた関数の定義域がはじめの関数のそれと共通部分が空でない場合,値は必ずしも一致しないのがふつうである。一致するための十分条件を与えるものに,次の1価性の定理がある。すなわち,Dで定義されたfが,Dを含む単連結領域Ω内の,すべての曲線に沿って解析接続が可能なとき,Ωで定まる関数は1価である。
一般には,解析接続の結果,多価関数を生ずる。のみならず,逆に解析接続は多価な正則関数を統一的に論ずるための重要な手段となっている。
→解析関数 →関数論
執筆者:及川 広太郎
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報

