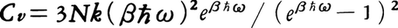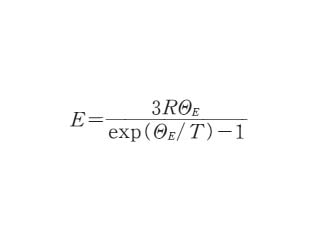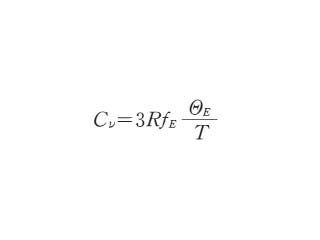アインシュタインの比熱式（読み）アインシュタインのひねつしき（英語表記）Einstein's formula for specific heat

改訂新版　世界大百科事典

アインシュタインの比熱式 (アインシュタインのひねつしき)
Einstein's formula for specific heat

固体の格子比熱と温度との関係を与える式。A.アインシュタインによって1907年に導かれた。固体は格子振動にエネルギーを蓄えることができるので，それに付随した比熱（格子比熱）をもっている。この比熱は，高温ではデュロン=プティの法則に従って一定値3Nk（Nは原子数，kはボルツマン定数。気体定数をRとすればNk＝R）をとるが，低温で急速に0になり，デュロン=プティの法則から大きくずれる。古典論では説明できないこの現象に対し，アインシュタインは一つ一つの原子を単振子とみなし，それに量子力学を適用して，単振子がħω（ħはプランク定数を2πで割ったもの，ωは単振子の角振動数）を単位とする不連続なエネルギーをもつと考えることによって，アインシュタインの比熱式と呼ばれる次の式を導いた。

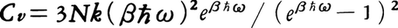
ここで，C_vは格子比熱（定積），Tは絶対温度で，β＝1/kTである。実験結果との一致は必ずしも十分とはいえないが，この式はそれまで説明が困難であった低温での格子比熱のふるまいに初めて説明を与えた。その後，デバイは単振子の振動を独立とせず波動として扱うことによって，より実験結果と一致するデバイの比熱式を導いた。
執筆者：小林 俊一

出典　株式会社平凡社「改訂新版　世界大百科事典」

法則の辞典

アインシュタインの比熱式【Einstein's equation of specific heat】

固体の元素単体のモル比熱が，デュロン‐プティの法則＊で示される3R よりかなりずれて小さな値となることを説明できるように，アインシュタインが導いた比熱式．N 個の同種原子からなる結晶の格子振動を，すべて共通の振動数 ν をもつ N 個の独立した三次元調和振動子の集合（つまりアインシュタインのモデル＊）と考える．この調和振動子の系が温度 T において熱振動しているものとして，そのエネルギーの平均値を統計力学によって求めると

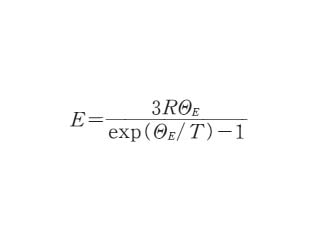
となる．これを温度 T で微分すると

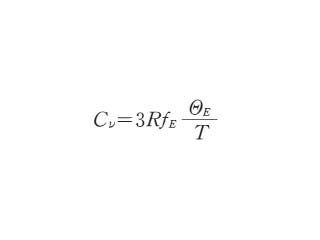
の形になる．ここで f_E（x）＝x²e^x/（e^x－1）² はアインシュタイン関数と呼ばれる関数である．もともと低温領域における比熱の異常性を解明するために考えられた式であるが，さらに低温となると不一致が大きくなり，この難点については後にデバイが改良を加えて新しい比熱式をつくった．デバイの比熱式＊の項も参照．

出典　朝倉書店

ブリタニカ国際大百科事典 小項目事典

アインシュタインの比熱式
アインシュタインのひねつしき
Einstein's specific heat formula

固体の定積比熱が低温においてデュロン＝プチの法則からずれることを説明するため 1907年 A.アインシュタインが提示した比熱式。固体の結晶の各原子が互いに独立に同じ振動数 ν で振動するというアインシュタイン模型を，統計力学の方法で処理して C_ν＝3Rx²e^x/(e^x－1)² という式を得た。ここで C_ν は定積モル比熱，R は気体定数，また x＝hν/kT であって h はプランク定数，k はボルツマン定数，T は絶対温度である。この式から，十分な高温では C_ν は約 3R で，デュロン＝プチの法則と一致し，低温では C_ν が非常に小さくなって定性的に実験と合う。のちに実験と定量的によりよく一致するデバイの比熱式が提示された。

出典　ブリタニカ国際大百科事典 小項目事典