近似式（読み）キンジシキ（英語表記）approximation formula

デジタル大辞泉

きんじ‐しき【近似式】

ある式の近似値の計算に都合のいい式。

出典　小学館

精選版 日本国語大辞典

きんじ‐しき【近似式】

1. 〘 名詞 〙 関数の値の近似値を求めるための数式。たとえば f(x)=x²+2x+1 に対し、ｘがきわめて小さいときには 2x+1 を近似式として用いることができる。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

近似式
きんじしき
approximation formula

(1)関数の計算を簡略化（高速化）するために使われる「代用の式」、(2)有限の時間内では厳密な関数計算ができない場合に使われる「真の関数値に近い値を算出する式」、(3)曲線や曲面の「概形を表す式」、の三つの意味がある。

［戸川隼人］

原理

適用範囲（独立変数の変域）をいくつもの区域に分け、一つの式でカバーする範囲を狭くすれば、低い次数の多項式、有理式、連分数などで近似できる。具体的には、(1)補間多項式を使う、(2)最小二乗法を使う、(3)テーラー級数を使う、(4)パデ展開（有理関数近似、すなわち多項式の比で近似する方式の一種）を使う、(5)連分数展開を使う、などの方法がある。また、最良近似の理論を応用すれば、より高精度で計算効率の優れた近似式を得ることができる。

　たとえば、対数関数の近似式をつくるには、log(1＋x)の無限級数展開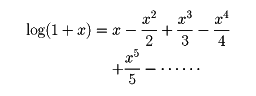

を適当な項数で打ち切って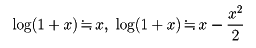

とする方法がまず考えられるが、xの絶対値が小さくないと、これではよい近似値が得られない。適用範囲がもっと広い改良された公式、たとえば
　log(1＋x)≒0.9974442x－0.4712839x²
　＋0.2256685x³－0.0587527x⁴
を用いれば、0≦x≦1の範囲で誤差8×10^-5以下の近似値を得ることができる。

［戸川隼人］

最良近似

近似式は、できるだけ誤差が少なく、計算の手間が少なく、適用できる範囲が広いことが望ましい。そのような観点から「近似の良さの総合的な尺度」を設け、近似式の係数を調整して最良の近似式を求める方法が研究されている。

　古典的な手法としては最小二乗法がある。これは近似式の形と適用範囲を固定し、誤差の二乗和（誤差の二乗を適用範囲全域にわたって積分したもの）が最小になるように係数を決める手法である。

　しかし、関数を近似する、という目的のためには、適用範囲内における誤差の最大値を最小にすることのほうが望ましい。これを「ミニマクス近似」という。

［戸川隼人］

標準的な関数の近似式

三角関数、逆三角関数、指数関数、対数関数、平方根、立方根、誤差関数、楕円(だえん)関数、ガンマ関数、ベッセル関数などに関しては優れた近似式が知られている。

［戸川隼人］

近似式を利用する際の注意事項

近似式は、普通、関数の値を近似するものであって、関数の変化率までは近似していない。したがって、近似式を微分した式を導関数の近似式として利用することはできない。関数の値だけでなく導関数の値も近似したい場合には、それ専用の手法（スプライン近似）を用いる必要がある。

［戸川隼人］

『藤野精一著『アルゴルとフォートランの応用』（1971・朝倉書店）』▽『ヘースティングス著、竹内均訳『電子計算機のための近似計算法』（1973・東京図書）』▽『一松信著『初等関数の数値計算』（1974・教育出版）』▽『高橋磐郎・室谷義昭著『数値計算とその応用』（1979・コロナ社）』▽『浜田穂積著『近似式のプログラミング』（1995・培風館）』

[参照項目] | ガンマ関数 | 逆三角関数 | 誤差関数 | 最小二乗法 | 三角関数 | 指数関数 | 対数関数 | 楕円積分 | テーラー級数 | 微分法 | 平方根 | 補間法 | 連分数

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

近似式 (きんじしき)
approximate expression

関数の値を計算する場合，正確な値を求める代りに，必要な精度をもつ関数を適当に選んで計算を容易にするほうが便利なことが多い。この目的のために用いられる関数を近似式，あるいは近似関数という。したがって，近似手法やそれに伴う誤差の評価が問題になる。近似式として多項式がよく用いられているが，これは多項式の値が計算しやすいうえ，多項式の和，差，積や導関数や不定積分がまた多項式になる利点による。例えばe^xをn次多項式で近似する場合，x＝0におけるテーラー展開を利用して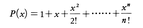，を近似式とすれば，誤差は，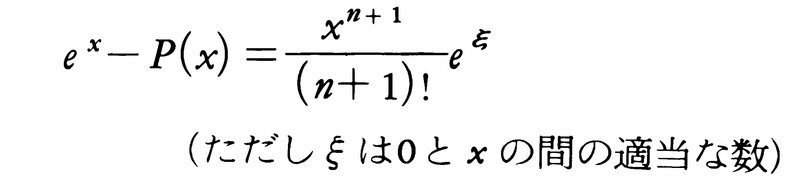

となり，xが0に近いときにはよい近似を与えるが，0から離れると近似も悪くなり，有効な方法といえない。区間［a，b］上の関数fをn次多項式Pで近似する場合，目的に従って誤差の測り方を定めて，誤差を最小にするようにPを選ぶ必要がある。誤差の基準は幾とおりかあるが，最大誤差や2乗積分誤差がよく用いられる。（1）ミニマックス近似　連続関数fを［a，b］上で一様に近似したい場合，最大誤差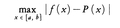，を小さくするように近似式を選ぶ。すなわち，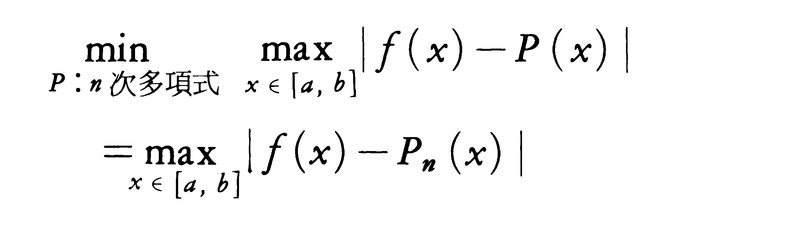

となるn次多項式P_nをミニマックス近似多項式と呼ぶ。［a，b］上の連続関数は多項式で近似できる（ワイヤーシュトラスの多項式近似）から，P_nによる最大誤差は，n→∞のとき0に収束する。具体的にP_nを求めることはむずかしい問題になる。

（2）最小2乗近似　2乗積分誤差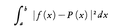，を最小にするように近似式を選ぶ。すなわち，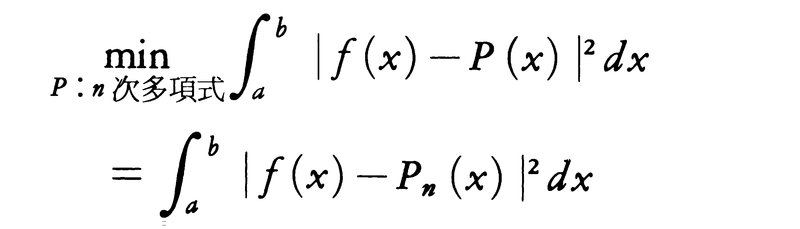

となるn次多項式P_nを最小2乗近似多項式と呼ぶ。1，x，……，xⁿの直交化により，P_nを具体的に求めることができ，さらにn→∞のときP_nによる誤差は0に収束する。目的によっては，有理関数を近似関数として用いることも多い。
執筆者：西尾 真喜子

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

近似式
きんじしき
approximate expression

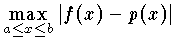関数 f(x) の値の近似値を求めるために使われる計算に便利な式を，一般に f(x) の近似式という。関数 f(x) が微分可能で，f'(x) が連続ならば，x が a に近い値，たとえば x＝a＋h のときの関数 f(x) の値は，式 f(x)≒f(a)＋f'(a)(x－a) によって近似できる。この式が関数 f(x) の近似式である。たとえば，h＞0 が1に比べて十分に小さいとき，(1＋h)ⁿ の近似式は，(1＋h)ⁿ≒1＋nh である。一般に f(x) が n＋1 回微分可能ならば，マクローリン展開が近似式になる。しかしこれらは展開中心の近傍でしか有用でない。広い範囲にわたる場合には，区間 [a，b] において，n 次多項式 p(x) のうち，差の最大値 を最少にするというようなミニマックス近似，あるいは最良近似を使うのが普通である。

出典　ブリタニカ国際大百科事典 小項目事典