デザルグの定理（読み）でざるぐのていり

日本大百科全書(ニッポニカ)

デザルグの定理
でざるぐのていり

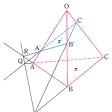
底面の三角形ABCが平面π上にある四面体O‐ABCを他の平面π′で切ると、図Aのようにπ′上に三角形A′B′C′ができる。このとき点P、Q、Rは平面π上にもπ′上にもあるから、当然π、π′の交わりである直線g上にある。この四面体を適当な方向から写真に撮れば図Bとなる。デザルグの定理は図A・図Bが表す次の定理である。「△ABC,△A′B′C′において、対応辺BCとB′C′、CAとC′A′、ABとA′B′の交点P、Q、Rが一直線上にあれば、対応する頂点を結ぶ三直線AA′、BB′、CC′は一点に会する。」
　ここでは無限遠点を導入した平面または空間について述べたから、たとえば辺BCとB′C′とが平行ならば、それらの交点Pとは直線BC上の無限遠点の意味である。「点Pが直線g上にある」とか、「直線gが点Pを通る」という関係を結合関係といい、幾何学のもっとも原始的な関係である。デザルグの定理はこの結合関係に関する基本的定理である。図Aは、三角形ABCを点Oから射影し、平面π′で切断したと考えられる。このような射影と切断で変わらない性質を研究するのが射影幾何学であり、結合関係や非調和比は射影幾何学的性質である。デザルグは射影幾何学の端緒を開き、また平行線は無限遠点で交わると考えて幾何学に初めて無限遠の考えを導入した。デザルグの定理の図Bは10個の（交）点と10本の直線よりなり、各（交）点をそれぞれ3本の直線が通り、各直線上にはそれぞれ3個の（交）点があるというおもしろさもある。

［立花俊一］

[参照項目] | 射影幾何学

デザルグの定理説明図〔図A〕

デザルグの定理説明図〔図B〕

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

デザルグの定理
デザルグのていり
Desargues's theorem

デザルグの三角形定理ともいう。射影幾何学における最も基本的な定理。一つの平面上に，2つの三角形 ABC と A'B'C' があるとき，その対応する頂点をそれぞれ結んでできる直線 AA' ，BB' ，CC' が1点O で交わるならば，対応する辺 BC と B'C' ，CA と C'A' ，AB と A'B' のそれぞれの交点P ，Q ，R は1直線 l 上にある。この定理は，空間における2つの平行でない平面上の三角形についても成立する。このような関係におかれた2つの三角形を，配景の位置にあるデザルグの図形といい，O を配景の中心，l を配景の軸という。これらをまとめると，定理は「空間または同一平面上に，ある2つの三角形 ABC および A'B'C' があるならば，対応辺 BC と B'C' ，CA と C'A' ，AB と A'B' のそれぞれの交点は1直線上にある」と述べられる。 G.デザルグは，この定理において，BC と B'C' が平行な場合を取上げ，これら2直線は「無限遠点」で交わると述べている。3次元の場合は △ABC を含む平面と △A'B'C' を含む平面との交わりを考えれば簡単であるが，平面の場合は特別の意味をもち，一般の射影幾何としては，デザルグの定理の成り立たないような非デザルグ射影平面がある。

出典　ブリタニカ国際大百科事典 小項目事典

改訂新版　世界大百科事典

デザルグの定理 (デザルグのていり)

射影幾何学の基本定理である次の定理およびその逆を合わせてデザルグの定理という。〈三角形ABCと三角形A′B′C′において，対応する頂点を結ぶ3直線が1点で交わるならば，対応する辺の交点である3点は1直線上にある〉。この定理は三角形が空間にある場合にも平面上にある場合にも成り立つが（図1，2），平面上の場合にも空間で考えれば点，直線，平面の間の結合に関する性質だけを用いて容易に証明することができる。しかしながら，平面上のデザルグの定理を平面上だけで証明するにはどうしても計量に関する性質を必要とすることが知られている。このように空間でのデザルグの定理と平面上でのデザルグの定理の間には根本的な性格上の相違があり，このためにデザルグの定理は幾何学の基礎論でもきわめて重要なものとなっている。
執筆者：中岡 稔

図1～図2

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内のデザルグの定理の言及

【幾何学】より

…デザルグやパスカルは，無限遠点やそれらの集りである無限遠直線を考えれば，ギリシア人が個々別々に陳述し証明した事柄が，統一的，かつ普遍的に得られることをいろいろな例によって示した。これらの中に，〈二つの三角形の対応する3頂点を結ぶ直線が1点で交われば，対応する辺の交点は1直線上にあり，この逆も成り立つ〉というデザルグの定理や，〈円錐曲線に内接する六角形の相対する辺，またはその延長の交点は1直線上にある〉というパスカルの定理がある。デザルグやパスカル以後は，解析幾何学や微積分学の華々しい進展の陰に隠れて，射影的方法による幾何学の研究は忘れられていたが，18世紀末にG.モンジュによって透視図法が復活されたのをきっかけとして，19世紀前半には射影的方法による幾何学の組織的研究が行われ，射影幾何学と呼ばれる数学の一分科が成立した。…

※「デザルグの定理」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」