ベン図（読み）ベンズ

デジタル大辞泉

ベン‐ず〔‐ヅ〕【ベン図】

《Venn diagram》集合の関係をわかりやすくするため、全体集合を長方形で、部分集合を円で表した図。英国の論理学者ベン（J.Venn）が創始。

出典　小学館

精選版 日本国語大辞典

ベン‐ず‥ヅ【ベン図】

1. 〘 名詞 〙 ＝ベンのずしき（━図式）②

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

ベン図
べんず

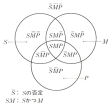
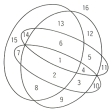
論理における推論を図形的に表すもので、オイラーの図式を修正してベンJohn Venn（1834―1923）が導入（1880）した。「SはMである」「MはPでない」という二つの前提が与えられたとする。このとき、三つの円を、可能なすべての重なりをもつように書いて、平面を八つの領域に分ける。それぞれの円をS、M、Pと名づける。Sの内部の点はSを、Sの外部の点はSの否定を表す。他の円についても同様である。八つの領域について、空である領域に斜線を書く。「SはMである」から、Mの外部のSの部分に斜線を書く。「MはPでない」から、Pの内部のMの部分に斜線を書く。その結果、Sの斜線のない部分はPの斜線のない部分の外部にあり、「SはPでない」ことが推論される。次に、空でないことがわかった領域には×印をつける。空でない領域が、隣接した二つの領域のいずれかがわからないときは、×印をその境界上に書く。「あるSはMである」とする。このとき、Sの内部の、MとPの境界上に×印が書かれ、「MはPである」とすると、×印はS、M、Pの共通部分の内部に移り、「あるSはPである」ことが推論される。四つの場合には円のかわりに楕円(だえん)を用いて、平面を16の領域に分ける。これでかなり複雑な推論も図で表すことができるが、五つ以上の場合には、一見して理解することはきわめて困難になるので、数が多いときには、行列状の四角形を用いる。

［西村敏男］

[参照項目] | オイラーの図式

ベン図（三つの円を用いた場合）

ベン図（四つの楕円を用いた場合）

ベン図（行列状の四角形を用いた場合）

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

ベン図 (ベンず)

→集合

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内のベン図の言及

【集合】より

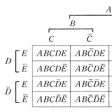
…共通部分，合併集合などを考えるとき，図のように集合を象徴的に表すと便利なことがある。このような図をベン図またはベンJ.Venの図式という。　Aが集合Mの部分集合であるとき，｛x∈M｜x∉A｝をAのMにおける補集合といい，A^c,M―A,M╲A，Āなどの記号で表されることが多い。…

※「ベン図」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」