ポインティングベクトル（英語表記）Poynting's vector

デジタル大辞泉

ポインティング‐ベクトル（Poynting's vector）

電磁波のエネルギーの流れを表すベクトル。その大きさは、電磁波の進行方向に垂直な単位面積を単位時間に通過するエネルギーに等しい。英国の物理学者ポインティングによって導入された。

出典　小学館

改訂新版　世界大百科事典

ポインティングベクトル
Poynting's vector

真空中では磁束密度B，電場Eの間には，真空の誘電率および透磁率をそれぞれε₀，μ₀，時間をtで表すと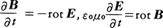，の関係がある（マクスウェルの方程式）。したがって，電場および磁場のエネルギー密度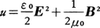，の時間変化は，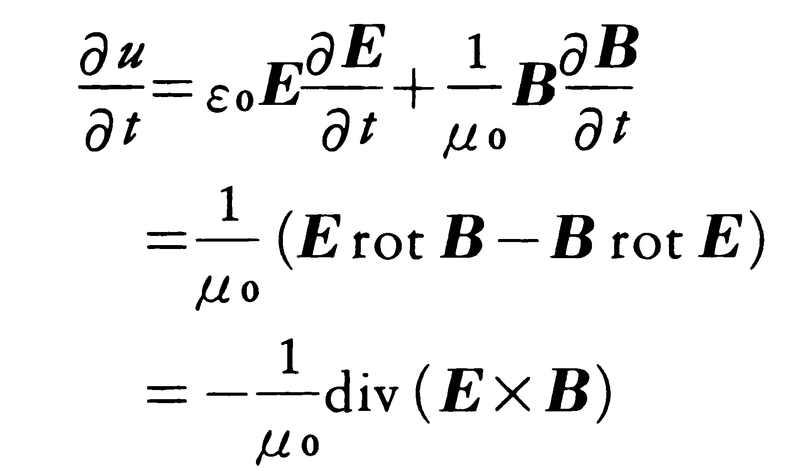

と表される。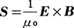とすると，Sの発散，すなわちdivSは，電磁場のエネルギーの減少－∂u/∂tを表していることになる。ガウスの定理を使うと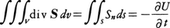，となるから（S_nはS上でのSの法線成分），ある曲面Sにかこまれた体積V中のエネルギーの減少－∂u/∂tは，この体積の表面上でのS_nの積分に等しくなる。この意味でSはエネルギーの流れを表しており，このSをポインティングベクトルと呼ぶ。イギリスの物理学者ポインティングJohn Henry Poynting（1852-1914）によって導入されたことからこの名がある。
執筆者：清水 忠雄

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

ポインティング・ベクトル
ぽいんてぃんぐべくとる
Poynting's vector

1884年にイギリスのポインティングが与えた電磁場におけるエネルギーの流れを示すベクトル。電場Eと磁場Hとが、空間のある同じ位置r、同じ時刻tで共存する場合には、ベクトルS(r,t)=E(r,t)×H(r,t)を考えることができる。このベクトルをポインティング・ベクトルという。ポインティング・ベクトルの物理的意味は、ある閉曲面を考えて、その面上または面内の体積でポインティング・ベクトルを積分したときに初めて現れる。すなわち、表面積分

は、考えている閉曲面の表面を通って、単位時間当りに流れる電磁場のエネルギーを表す。積分値の符号によって、閉局面から流出するエネルギーと区別することができる。また、同じ閉局面で囲まれた領域での体積積分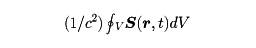

は、この領域内に存在する電磁場の運動量ベクトルを表す。

　電磁場のエネルギーや運動量は、けっして抽象的なものではなく、物質の力学的なエネルギーや運動量と同等の物理量である。すなわち、荷電粒子と電磁場とが相互作用している系においては、荷電粒子のエネルギーや運動量ばかりでなく、電磁場のエネルギーや運動量を考慮に入れて初めて、系全体の物理現象が正しい物理法則に従う。

［安岡弘志］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

ポインティング・ベクトル
Poynting's vector

電場 E ，磁場 H があるとき，E×H で定義されるベクトル。電磁場のエネルギーの流れを表わす。電磁波の場合，単位面積についてポインティング・ベクトルの方向に ｜E×H｜ だけのエネルギーが流れている。またポインティング・ベクトルを c² ( c は光速度) で割ったものは電磁場の運動量密度である。

出典　ブリタニカ国際大百科事典 小項目事典

法則の辞典

ポインティングベクトル【Poynting vector】

電場を E，磁場を H としたとき，S＝E×H で定義されるベクトル．電磁場のエネルギーを表現する．

出典　朝倉書店

世界大百科事典（旧版）内のポインティングベクトルの言及

【光】より

…これは，単位時間に単位面積を通過する光子数にhνを乗じたものに等しい。またS＝E×Hで定義されるベクトルSをポインティングベクトルといい，Sの方向が光の進行方向，その大きさが光の強度を与える。透磁率と誘電率とがμとεとである物質中では，放射インピーダンス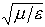は光の速さは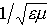となるが，光の振動数はきわめて大きいので，通常の物質ではμ＝μ₀としてよく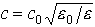，と表せる(ただし，この場合εは光の振動数に依存すると考えなければならない)。…

※「ポインティングベクトル」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」