モンテカルロ法(モンテカルロホウ)とは？意味や使い方

デジタル大辞泉「モンテカルロ法」の意味・読み・例文・類語

モンテカルロ‐ほう〔‐ハフ〕【モンテカルロ法】

《Monte Carlo method》乱数を用いたシミュレーションを何度も行って、近似的な解を得る数値計算の手法。解析的なアプローチが困難な場合などに用いられる。高い精度の解を得るためには、試行回数を増やす必要がある。モンテカルロシミュレーション。MC法。

出典　小学館デジタル大辞泉について　情報 | 凡例

Sponserd by

精選版日本国語大辞典「モンテカルロ法」の意味・読み・例文・類語

モンテカルロ‐ほう‥ハフ【モンテカルロ法】

〘名詞〙 ( モンテカルロのカジノで行なわれる賭博の勝敗の確率計算に由来する名称 ) 数学における問題解決法の一つ。確率的な実験を利用するもので、計算では容易に処理できない問題を解くのに用いられる。

出典　精選版日本国語大辞典精選版日本国語大辞典について　情報 | 凡例

Sponserd by

改訂新版　世界大百科事典「モンテカルロ法」の意味・わかりやすい解説

モンテカルロ法 (モンテカルロほう)
Monte Carlo method

乱数あるいは物理的なランダム・メカニズムを使った実験によって数学的な問題の近似的な数値解を得る方法。名前はカジノで有名なモナコの都市モンテ・カルロに由来する。この方法が実用的な問題の解決に使われたのは，1940年代の中ごろ，フォン・ノイマンらによるのが最初で，命名も彼らによるとされている。本来は，確率的な変動要因を含まない問題を解くのに確率論的な手法（乱数）を使う方法に対して与えられた名称であるが，現在では乱数を使う方法の総称として使われることが多い。

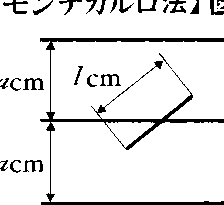
　実用的ではないが，古典的で有名な例としては，G.L.L.ビュフォンの針の問題がある。図のように等間隔（間隔acm）に並んだ平行線群の上に長さlcmの針をN回落とし，針が平行線と交わった回数nを数えるという実験を行う。針を1回落としたときにそれが平行線と交わる確率は2l/（aπ）であり，したがってNを非常に大きくすれば，大数の法則により，n/Nはこの確率に近いことが期待される。すなわちn/N≒2l/（aπ）。これからπ≒2lN/（an）となり，右辺の値を計算することによって円周率πの近似値が求められる。最近になって，この原理はもっと実用的な問題－－地図上の多数の道路の総延長を測るという問題－－に応用された。この場合には，道路は折れ線（線分の集り）で近似できるものと考え，πの値は既知として，l≒πan/（2N）という関係式によって線分の長さlの近似値を求めていることになる。

　以上の例では，針を落とすというような物理的なメカニズムを使っているが，このようなやり方だと多数回の実験をするためにはきわめて長時間を要するので，通常はコンピューターの中で高速に多数の乱数を作り出して使っている。

　モンテカルロ法の欠点は，精度のよい近似解を得るのが困難であるという点にある。すなわち，近似値の精度を1けた増やそうとすると，試行の回数を100倍にしなければならない。たとえばπの近似値を2けたの精度で求めるのは比較的容易であるが，6けた程度まで求めようとすると1兆回以上も試行をしなければならず，高速のコンピューターを用いたとしてもきわめて長時間を必要とする。しかし，あまり詳しい数値を必要とせず，だいたいの傾向がわかれば十分であるような問題に対しては，便利で適用範囲の広い方法である。つぎにあげるのは，適用された問題のいくつかの例である。（1）原子物理学，特に原子炉の設計や臨界値の計算。（2）連立一次方程式の解や逆行列の計算。（3）定積分，特に多重積分の計算。（4）液体や気体中の粒子の運動の解析。（5）固体の中へ液体が浸透する現象の解析。（6）さまざまな物理的現象が偏微分方程式によって記述されるが，その解を求めること。

　最近になって，デリバティブ（金融派生商品）の価格評価等の分野では，大規模な問題に対する解を，かなりの精度で，しかも短時間に出したいという要望が出されるようになった。このため，乱数の代りに準乱数と呼ばれる特別な数を使用する準モンテカルロ法という方法も使われるようになってきた。
執筆者：伏見正則

出典　株式会社平凡社「改訂新版　世界大百科事典」改訂新版　世界大百科事典について　情報

Sponserd by

日本大百科全書(ニッポニカ) 「モンテカルロ法」の意味・わかりやすい解説

モンテカルロ法
もんてかるろほう

1940年代のなかばごろ、ノイマンとウラムによって提案された数学的方法で、簡単にいえば問題を乱数を用いて解く方法である。

　古典的なビュフォンの針の問題は、考え方としてはモンテカルロ法の一例といえる。床の上に2aの間隔で平行線を何本も引いておき、上から長さ2l（l＜a）の針を落とすと、針が平行線と交わる確率pはp＝2l／aπとなる。そこで針を落とす実験をN回行って落ちた針が平行線と交わった回数がnであれば、n/Nをpの近似値とみることができる。こうしてπ≒2lN/anからπの近似値を実験によって求めることができる。これがビュフォンの針の問題である。

　モンテカルロ法の応用は次の二つに大別される。一つは確率的問題への応用であり、もう一つは決定論的問題への応用である。確率的問題ではそれを直接表現する確率モデルを考える。たとえば、在庫管理の問題では需要が確率的に変化し、待ち行列の問題では客の到着状態やサービス時間が確率的に変動する。これらのモデルにおいて確率的な部分を乱数を用いて表現して問題の解を実験的に求めることができる。決定論的問題では、まず、その問題に対応する適当な確率モデルを設定する。ビュフォンの針の問題はこの型である。また、逆行列を数値的に求めること、定積分の値を数値的に求めること、偏微分方程式の境界値問題の数値解を求めることなど、多くの決定論的問題に対しても確率モデルを考え、確率的問題の場合と同様に乱数を用いて問題を解決することができる。しかし直接に（確率モデルを経由しないで）数値計算が可能な場合には、そのほうがモンテカルロ法より効果的のようである。最近では、乱数を用いて計算機によるシミュレーションで解く方法をモンテカルロ法とよんでいる。

［古屋　茂］

[参照項目] | シミュレーション

出典　小学館　日本大百科全書(ニッポニカ)日本大百科全書(ニッポニカ)について　情報 | 凡例

Sponserd by

百科事典マイペディア「モンテカルロ法」の意味・わかりやすい解説

モンテカルロ法【モンテカルロほう】

解析学の問題のように確率を伴わない数学的問題を，これに対応する実際的な確率過程の問題におきかえて解決する方法。たとえば等間隔で多数の平行直線を引き，その間隔と同じ長さの針をでたらめに多数回おとすと，針が線と交わる回数は全体の2/πになることが確率的に計算できる。そこで実際に針を投げて線と交わる回数を数え，それの結果からπの近似値を算出することができる（ビュフォン，1773年）。最近コンピューターと乱数を用いシミュレーションにより問題を解く方法が発達し，広く利用されている。
→関連項目オペレーションズリサーチ

出典　株式会社平凡社百科事典マイペディアについて　情報

Sponserd by

化学辞典第2版「モンテカルロ法」の解説

モンテカルロ法
モンテカルロホウ
Monte Carlo method

数学や物理学などの問題を解くとき，統計的な標本抽出法を用いて近似解を求める方法．たとえば，複雑な図形の面積を求めるとき，原則的には図形を分解して定積分によって求めることができる．しかし，この作業は非常に時間がかかる．これを避けるために，図形を含むある範囲を設定し，この範囲すべてを均等な細かい断片に分割して，統計的に取り扱える回数だけ任意にサンプリングを行う．図形の断片をサンプリングした回数とサンプリング総数の比を範囲の全面積にかければ，図形の面積の近似値を求めることができる．モンテカルロ法は，実際的であるが，精度を上げるのは難しく，つねに求めた解の信頼性に注意しなければならない．計算化学における各種の分子シミュレーションに用いられている．

出典　森北出版「化学辞典（第2版）」化学辞典第2版について　情報

Sponserd by

ブリタニカ国際大百科事典小項目事典「モンテカルロ法」の意味・わかりやすい解説

モンテカルロ法
モンテカルロほう
Monte Carlo method

決定論的および確率論的事象の処理について，乱数を用いる無作為抽出により，数値化，模型化して問題の近似解を導く方法。地中海に面したモナコのモンテカルロにおける賭博にまねて1種のルーレットによる乱数を使用するために名づけられた。簡単な処理や事務には乱数表がよく利用される。現在は複雑な事象に関して，電子計算機により多数の乱数を発生させ，サンプリングを能率化する。宇宙線のカスケードシャワーの問題，原子炉内における中性子の経路問題，社会における待合せ問題，ランダムウォーク問題，企業における在庫量管理の問題などの確率的事象として処理すべき多様な事項に応用される。

出典　ブリタニカ国際大百科事典小項目事典ブリタニカ国際大百科事典小項目事典について　情報

Sponserd by

会計用語キーワード辞典「モンテカルロ法」の解説