ユークリッドの互除法（読み）ユークリッドノゴジョホウ（英語表記）Euclidean algorithm

デジタル大辞泉

ユークリッド‐の‐ごじょほう〔‐ゴヂヨハフ〕【ユークリッドの互除法】

二つの整数の最大公約数を求める算法。大きい方の数を小さい方の数で割り、その剰余で小さい方の数を割る演算を繰り返す。最後に残る除数が求める最大公約数となる。二つの整式についても成り立つ。ユークリッドの著書「ストイケイア」に記載。互除法。

出典　小学館

精選版 日本国語大辞典

ユークリッド の 互除法(ごじょほう)

1. 二つの整数の最大公約数を求める方法の一つ。ユークリッドの「幾何学原本」に記載されているもの。互除法。

出典　精選版 日本国語大辞典

ブリタニカ国際大百科事典 小項目事典

ユークリッドの互除法
ユークリッドのごじょほう
Euclidean algorithm

二つの自然数 a₁と a₂の最大公約数（→約数）を求めるための一つの方法。a₁≧a₂として，次の割り算を実行する。

a1＝a2q1＋a3		q1は商，a3は余り
a2＝a3q2＋a4		q2は商，a4は余り
…………		…………
an-1＝anqn-1＋an+1		qn-1は商，an+1は余り
an＝an＋1qn		qnは商，余りはなし

最後に余りがなかったならば，この a_n+1が最初の 2数 a₁と a₂の最大公約数である。（→整数論，ユークリッド）

出典　ブリタニカ国際大百科事典 小項目事典

改訂新版　世界大百科事典

ユークリッドの互除法 (ユークリッドのごじょほう)
Euclidean algorithm

二つの自然数の最大公約数を見つける方法。二つの自然数a，bが与えられているとする。a≧bとして，aをbで割ったときの余りをa₁とする。bをa₁で割り，その余りをb₁とおく。b₁でa₁を割り，余りをa₂とする。このようにして，a≧b＞a₁＞b₁＞a₂＞b₂＞……となる整数の列が定まっていくが，どこかで0になる。そのすぐ前の自然数がaとbの最大公約数である。例えば，a＝63，b＝49ならば，a＝63，b＝49，a₁＝14，b₁＝7，a₂＝0となり7が最大公約数である（図1）。この方法は1変数の多項式にも有効である。1変数の多項式の大きさを次数で比べて，割って余りを取る方法を繰り返せばよい。例えばf＝x⁴＋x³＋x＋1，g＝2x³＋5x²＋4x＋1の場合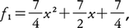g₁＝0となり，最大公約式はx²＋2x＋1である（図2）。この方法は《ストイケイア》に書かれているので，ユークリッドの互除法といわれるようになった。
執筆者：丸山 正樹

図1～図2

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

ユークリッドの互除法
ゆーくりっどのごじょほう

最大公約数を求める方法。a₁、a₂を自然数あるいは整式とする。自然数のときは、a₁≧a₂で、整式のときは、a₁の次数のほうがa₂の次数以上であるとする。

　　a₁=a₂q₁+a₃　（a₃は剰余）
　　a₂=a₃q₂+a₄　（a₄は剰余）
　　　　…………
　　a_n-1=a_nq_n-1+a_n+1
　　　　　　　 　（a_n+1は剰余）
　　a_n=a_n+1q_n
となるとき、a_n+1がa₁とa₂の最大公約数である。a_n+1=1のときは、a₁とa₂は互いに素である。3553と2584の最大公約数は323であるが、これは次のようにして求める。

　　3553=2584×1+969
　　2584=969×2+646
　　969=646×1+323
　　646=323×2
［寺田文行］

出典　小学館　日本大百科全書(ニッポニカ)

ASCII.jpデジタル用語辞典

ユークリッドの互除法

自然数の最大公約数を効率よく求める方法。世界で最初のアルゴリズムといわれている。

出典　ASCII.jpデジタル用語辞典