リニアプログラミング（読み）りにあぷろぐらみんぐ（英語表記）linear programming

デジタル大辞泉

リニア‐プログラミング（linear programming）

⇒線形計画法

出典　小学館

精選版 日本国語大辞典

リニア‐プログラミング

1. 〘 名詞 〙 ( [英語] linear programming ) 企業経営における生産・輸送および長期にわたる経済計画などを最適にするのに用いられる数学的方法の一つ。制約条件をいくつかの一次の等式または不等式によって表わし、計画の効果をはかる尺度も一次式によって得られるもの。近代経済学の一方法。略称ＬＰ。線形計画法。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

リニア・プログラミング
りにあぷろぐらみんぐ
linear programming

一次の不等式または一次式で表される制約条件のもとで、一次式で表される目的関数あるいは評価関数を最大（または最小）にする最適化技法の一つ。一次式はグラフにすると直線（線形）になるので、線形計画法ともいう。略称LP。たとえば、ある工場で2種類の製品（AとB）を2台の機械（M₁とM₂）を使って生産する場合に、最大の利益（z）をあげるには各製品をどのくらい生産するかを決定する問題は、次の例で示すように、リニア・プログラミングの問題として定式化できる。いま、表に示すような各製品を生産するために必要な時間および制約と利益が与えられている場合を考える。製品Aの生産量をx_A、また製品Bの生産量をx_Bとすれば、リニア・プログラミングの問題は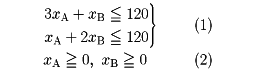

という制約条件のもとで、次に示す目的関数
　　z=2x_A+x_B　(3)
を最大になるような決定変数x_Aとx_Bを求めることである。ここで、式(2)を非負条件という。

　ここでのLP問題のように、決定変数が2個（x_A,x_B）の場合には、平面上に式(1)のグラフを書くことができ、図のようになる。この図で、斜線部分が制約条件(1)と非負条件(2)を満足するx_A、x_Bの範囲を表し、実行可能域とよんでいる。LP問題の実行可能域は、一般に図のような凸多角形の内部とその辺上になる。したがって、実行可能域内の点（x_A,x_B）で目的関数(3)を最大にするのは、点Bすなわちx_A=24,x_B=48であり、その利益は96万円となる。このように、線形計画問題では、目的関数値は凸多面体の端点で最大または最小値をとることが知られている。このようなLP問題を解くおもな手法としては、1950年代の後半に、ダンツィグGeorge B. Danzig（1914―2005）が開発したシンプレックス法（単体法ともいう）や改訂シンプレックス法などがある。これらの手法のコンピュータ・プログラムが開発されて以来、リニア・プログラミングは広く生産管理、経営計画、在庫管理、石油の混合問題、栄養問題などによく使用されるようになった。

［玄　光男］

『玄光男・井田憲一著『BASICによる線形計画』（1988・共立出版）』▽『小山昭雄著『線形計画入門』（日経文庫）』

[参照項目] | 応用数学 | 最適化

リニア・プログラミングの例（製品の工数…

リニア・プログラミングの例（決定変数が…

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

リニアプログラミング
linear programming

→線形計画法

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

リニアプログラミング

→線形計画法

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

リニア・プログラミング

「線形計画法」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典

ASCII.jpデジタル用語辞典

リニアプログラミング

「線形計画法」のページをご覧ください。

出典　ASCII.jpデジタル用語辞典

世界大百科事典（旧版）内のリニアプログラミングの言及

【線形計画法】より

…リニアプログラミング，略称LP。数理計画法の一種。…

※「リニアプログラミング」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」