可算（読み）かさん（その他表記）enumerable
countable

精選版 日本国語大辞典

か‐さん【可算】

1. 〘 名詞 〙 自然数の集合と一対一の対応がつけられること。可付番。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

可算 (かさん)
enumerable
countable

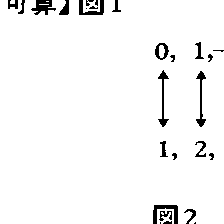
可付番ともいう。ある集合の元全体に1，2，3，4，……と自然数で番号をつけていくことができるとき，その集合は可算集合であるという。この定義では有限集合も許容されるが，無限集合に限定して使われる場合が多い。その場合は〈自然数の全体と1対1の対応をする集合を可算集合といい，その集合の濃度を可算という〉と定義すればよい。無限集合であることをはっきりさせるため可算無限ということもある。例えば整数全体は，図1のように番号をつけていくことができるので可算無限である。（x，y）平面で座標が整数である点（格子点）全体を考えると，図2のように矢印の方向に番号をつけていくことができるので可算無限である。一般に可算集合の無限部分集合は可算である。有理数を既約分数で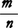（nは自然数）と表示して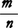，に（x，y）平面の点（m，n）を対応させると，有理数全体は（x，y）平面の格子点全体のなす集合の部分集合と1対1に対応する。したがって有理数全体の濃度は可算である。一方，実数全体の濃度は可算無限より真に大きい。可算無限は無限集合の濃度の中で最小のものであり，無限集合は必ず可算無限集合を部分集合として含んでいる。
→集合　→濃度
執筆者：上野 健爾

図1～図2

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

可算
かさん
denumerable; countable

可付番ともいう。無限の集合数のうち最小のもの。無限集合のすべての元と自然数の集合{1，2，3，…}との間に一対一対応がつけられれば，この集合は可算であるという。集合が可算であるとき，可算集合という。これは別の言葉でいえば，その集合の元を{ a₁ ，a₂ ，a₃ ，…，a_n ，…}のように列に並べた形で表示できる集合ということになる。たとえば，有理数全体の集合は可算集合である。

出典　ブリタニカ国際大百科事典 小項目事典