翻訳|identity
精選版 日本国語大辞典 「恒等式」の意味・読み・例文・類語
こうとう‐しき【恒等式】
- 〘 名詞 〙 数学で、その中の文字にどんな数値を代入しても常に成立するような等式をいう。
改訂新版 世界大百科事典 「恒等式」の意味・わかりやすい解説
恒等式 (こうとうしき)
identity
x3+y3=(x+y)(x2-xy+y2),1+tan2θ=sec2θのように,変数を含んだ等式で,その変数にどんな値を代入しても,両辺に意味がある限り(上の例では,第2式はcosθ=0となるようなθの値が除外される)等式が成り立つとき,その等式を恒等式という。ただし,変数の値の範囲は,通常実数全体であるが,複素数全体で考えることも,また後述のようにその他の場合もある。
(1)多項式による恒等式については,次のことが基本的である。
f(x),g(x)が一変数xについての数係数の多項式であり,次数がd以内であるとき,相異なるd+1個のxの複素数値a1,……,ad+1についてf(ai)=g(ai)が成り立てば,f(x)=g(x)は恒等式である。このことは,多変数の場合,次のように一般化される。
f(x1,……,xn),g(x1,……,xn)がn変数x1,x2,……,xnについての数係数の多項式であって,f,gとも,xiについての次数がdi以内であるとき,相異なるdi+1個の複素数からなる集合Si(i=1,……,n)を適当にとって,
ai∈Si (i=1,2,……,n)
f(a1,a2,……,an)=g(a1,……,an)
となるならば,f(x1,……,xn)=g(x1,……,xn)は恒等式である。したがって,次の系が得られる。
f(x1,……,xn),g(x1,……,xn)
h(x1,……,xn),k(x1,……,xn)
が数係数の多項式で,いずれも定数は0でないとする。このとき,
f(x1,……,xn)k(x1,……,xn)=g(x1,……,xn)h(x1,……,xn)
が恒等式であれば,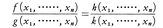 も恒等式であり,逆も成り立つ。
も恒等式であり,逆も成り立つ。
このことは,数係数,複素数の代りに,ある可換体Kを考え,Kに係数をもつ,Kの元にそれぞれおきかえても正しい。
(2)値が特殊な演算体系内を動くときにも,その体系についての恒等式という概念がある。そのようなもののうち有名なものは,それぞれの体系における演算公式ともいえるものである。
執筆者:永田 雅宜
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
ブリタニカ国際大百科事典 小項目事典 「恒等式」の意味・わかりやすい解説
恒等式
こうとうしき
identity
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
百科事典マイペディア 「恒等式」の意味・わかりやすい解説
出典 株式会社平凡社百科事典マイペディアについて 情報
世界大百科事典(旧版)内の恒等式の言及
【等式】より
…(1),(2),(3),(4)では両辺をそれぞれ適当に整理すると,両辺がまったく同じになり,等号はいつも成り立つ。このような等式を恒等式という。一方,(5),(6),(7)では,変数xやyに着目すると,xやyが特定の値をとるときにのみ等号が成り立つ。…
※「恒等式」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

