等式（読み）トウシキ（英語表記）equality

デジタル大辞泉

とう‐しき【等式】

二つの式または数を等号で結んだもの。

出典　小学館

精選版 日本国語大辞典

とう‐しき【等式】

1. 〘 名詞 〙 二つの数または式を等号で結んだもの。式に含まれている文字がある特定の値をとるときにのみ成り立つ方程式と、すべての値について成り立つ恒等式とがある。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

等式 (とうしき)
equality

数や変数，式，関数などについての式を等号で結んだものを等式という。例えば，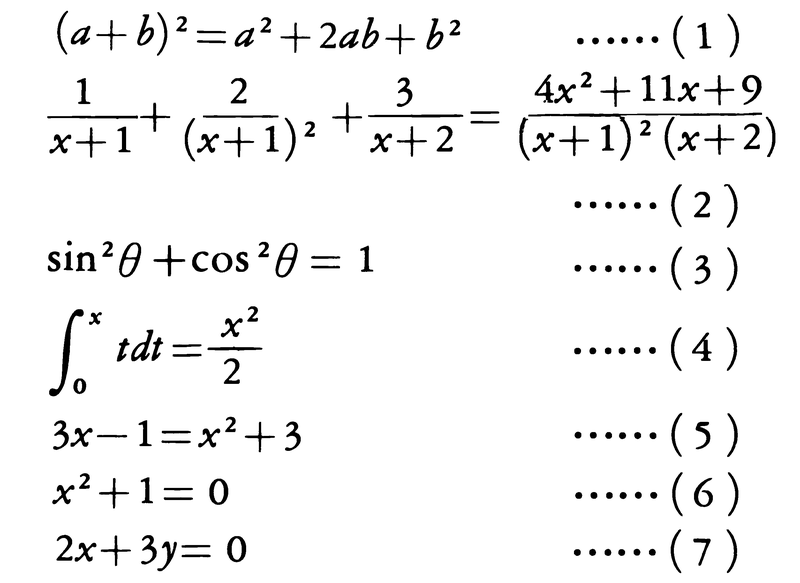

などは等式の例である。（1），（2），（3），（4）では両辺をそれぞれ適当に整理すると，両辺がまったく同じになり，等号はいつも成り立つ。このような等式を恒等式という。一方，（5），（6），（7）では，変数xやyに着目すると，xやyが特定の値をとるときにのみ等号が成り立つ。このような等式を方程式という。一般に，等式A＝Bは次の性質をもつ。

（1）A＝B，B＝CならA＝C

（2）A＝BならA±C＝B±C（複号同順）

（3）A＝BならAC＝BC

　A＝B，C≠0なら\(\frac{A}{C}\)＝\(\frac{B}{C}\)
執筆者：西村 純一

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

等式
とうしき
equation; equality

二つの数または式，あるいは数学的対象a，b があるとき，これらが等しいことを示すために記号＝（等号という）が用いられる。すなわちa＝b はa とb が等しいということを示している。この等しいという関係には，

(1)	a＝a	（反射律）
(2)	a＝b ならば b＝a	（対称律）
(3)	a＝b かつ b＝c ならば a＝c	（推移律）

という性質がある。等式とは，数や式が等号で結ばれている数学的表現のことである。等式には，恒等式と方程式がある。恒等式は，（a－b）²＝a²－2ab＋b² のようなもので，文字に値を代入することと無関係に，式の変形規則に従って証明される等式である。方程式は，3x－5＝0 のような式で，文字がある特定の値をとるときに限って成り立つような等式である。

出典　ブリタニカ国際大百科事典 小項目事典

日本大百科全書(ニッポニカ)

等式
とうしき

形式的には、二つの数学的対象（記号）を左右に置き、その間に等号を挟んだ式を等式という。左右の式をそれぞれ左辺および右辺という。等式の数学的意味は、左辺と右辺がともに同一の数学的対象を指示していることである。たとえば
　2+3=5,a+b=b+a,x²-3x-4=x+1,
　△ABC=△PQR
はすべて等式であり、第二の例はa、bがどんな数値を表すときでもつねに成り立つから、恒等式であり、第三の例はxが特定の数値（－1と5）を表すときだけ成り立つから、方程式である。また第四の例は左辺と右辺の三角形の面積が等しいことを表す。

　等号は同値関係の一種である。すなわち、A=A（反射的）、A=BならばB=A（対称的）、A=BかつB=CならばA=C（推移的）という三つの法則に従う。与えられた等式から数学的に導き出される等式を最初の等式の変形（変更）といい、この等式変形の原理は、前述の三法則と、A=BならばA±C=B±Cが成り立ち、またA=BかつC≠0ならば、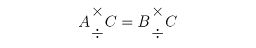

が成り立つことである。とくにA±B=CからA=C∓Bの変形を、左辺のBを右辺に移項するという。

　等式変形の原理（等式の性質）はとくに方程式の解法にとって重要である。

［竹内芳男］

出典　小学館　日本大百科全書(ニッポニカ)