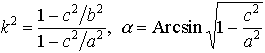楕円積分（読み）だえんせきぶん

日本大百科全書(ニッポニカ)

楕円積分
だえんせきぶん

Q(x)をxの三次または四次の式として、またR(x,u)をx、uの有理式として、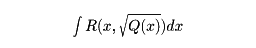

の形の不定積分で、初等関数（代数関数、指数関数、対数関数、逆三角関数など、微分積分学では基本的であると考えられる関数）で表すことのできないものを楕円積分という。楕円の弧長の計算に際して現れる積分なのでこの名がある。実際、楕円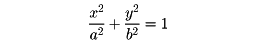

の弧の長さは、たとえば図のBからPまでだと、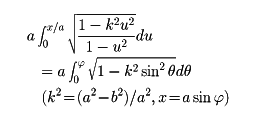

となり、k≠0ならば、初等関数で表すことはできない。このような積分は19世紀初めごろから注目された。

　楕円積分は、適当な変数変換により、初等関数と、次の形の不定積分の和となる。これをルジャンドル‐ヤコービの標準形という。ここで
　　0＜k＜1,　u=sinθ,
　　　x=sin
とする。

第1種楕円積分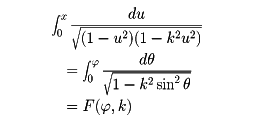

第2種楕円積分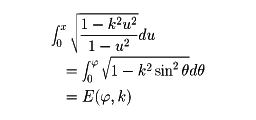

第3種楕円積分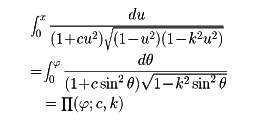

　第1種の楕円積分の逆関数をヤコービの楕円関数といってsnで表す。すなわち、この積分の値をzとして、x=snzである。snから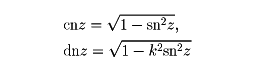

を定義する。楕円の周の全長は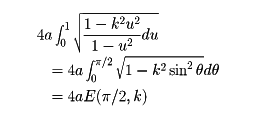

となる。この定積分、すなわちE(π/2,k)を第2種完全楕円積分という。同様に、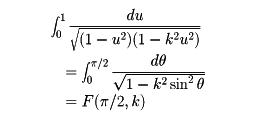

を第1種完全楕円積分という。楕円積分と同様に、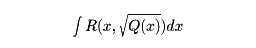

の形の積分で、Q(x)が五次式、六次式のときを超楕円積分という。これは、アーベル、ヤコービなどによって研究された。すでに述べたように、楕円積分の逆関数を楕円関数という。これは複素平面全体に解析関数として定義を拡張することができて、そのようにしたものは二重周期を有する周期関数であり、有理型関数である。

［竹之内脩］

楕円積分説明図〔図〕

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

楕円積分
だえんせきぶん
elliptic integral

x ，y を変数とする有理関数を R(x，y) とし，P(x) を x についての複素係数の3次または4次の多項式とするとき，積分
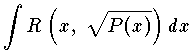は一般的に初等関数では表わせない。この形の積分を楕円積分を呼ぶ。楕円の周を計算しようとすると，この種の積分が現れるからである。しかし，例外的に初等関数で表わせる場合もあるが，そのときはこの形の積分を擬 (あるいは準) 楕円関数という。任意の楕円積分は，初等的な変換によって，初等関数と次の3種の積分のいずれかの和に帰着される。
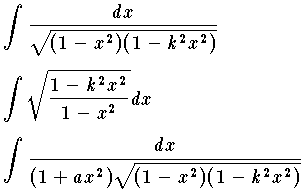ただし 0＜k＜1 である。この3種の積分をそれぞれ第1種，第2種，第3種の楕円積分といい，まとめてルジャンドル＝ヤコービの標準形という。 k を母数 modulusといい，第3種の場合の定数 a(a＞0) を，別変数あるいはパラメータと呼ぶ。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

楕円積分【だえんせきぶん】

xの３次または４次の多項式f（x）の平方根とxとの有理関数（式１）の積分。一般に初等関数では表せない。次の三つの積分（式２）のどれかに帰着され，それぞれ第１種，第２種，第３種の楕円積分という。楕円の弧の長さを計算するときこの積分が現れるので楕円積分と呼ぶ。→楕円関数／楕円面

出典　株式会社平凡社

世界大百科事典（旧版）内の楕円積分の言及

【楕円関数】より

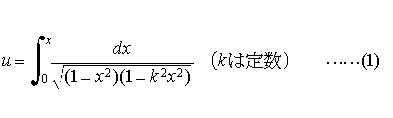…4点0,2ω₁,2ω₂,2ω₁＋2ω₂を頂点とする平行四辺形を基本周期平行四辺形という。　歴史的には，楕円関数の研究は，楕円積分に源をもつ。積分，のように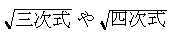の有理関数の積分のことを楕円積分という(楕円の周長を求める際に現れるのでこの名がついた)。…

【楕円面】より

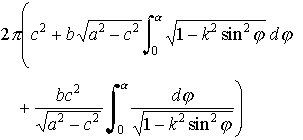…楕円面で囲まれた空間の部分を楕円体という。主軸の長さが2a,2b,2cのとき，楕円体の体積は4πabc/3で与えられ，a≧b≧cならば，楕円面の表面積は楕円積分を用いて次式で与えられる。ここに，二次曲面【中岡 稔】。…

※「楕円積分」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」