指数関数（読み）シスウカンスウ（英語表記）exponential function

デジタル大辞泉

しすう‐かんすう〔‐クワンスウ〕【指数関数】

aを1でない正の定数とするとき、関数y＝a^xを、aを底ていとするxの指数関数という。

出典　小学館

精選版 日本国語大辞典

しすう‐かんすう‥クヮンスウ【指数関数・指数函カン数】

1. 〘 名詞 〙 ａを１でない正の定数、ｘを変数とするとき、式 a^x で表わされる関数。ａをその底(てい)というが、自然対数の底ｅを底とする指数関数を単に指数関数と呼ぶことが多い。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

指数関数
しすうかんすう
exponential function

a＞0, a≠1として、y＝a^xで表される関数で、aを指数関数の底(てい)という。xが1, 2, 3のような自然数のとき、a^xはaの累乗、すなわちaをx回掛け合わせたものである。

　　a¹＝a,　a²＝a×a,
　　a³＝a×a×a,……
x＝0については、a⁰＝1と定める。たとえば3⁰＝1である。xが負の整数のときは、a^x＝1/a^-xと定める。たとえば、
　　10^-1＝1/10＝0.1,
　　5^-2＝1/5²＝0.04
となる。以上、整数値xについて定められたa^xに対して、次の指数法則が成り立つ。

(1)a^x・a^y＝a^x+y
　　　たとえばa⁵×a⁴＝a⁹
(2)(a^x)^y＝a^xy
　　　たとえば(2³)²＝2⁶＝64
(3)(ab)^x＝a^xb^x
　　　たとえば6³＝(3×2)³
　　　　　　　　＝3³×2³
　xが有理数のとき、x＝n/m（nは整数、mは正の整数）として、a^xはaⁿのm乗根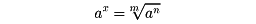

と定める。この拡張された指数についても、指数法則はそのまま当てはまる。たとえば、
　　8^2/3＝(2³)^2/3＝2^3×2/3＝2²＝4
　xが実数のときa^xを定義するには、次のような考察をする。いまa＞1としておく。このとき、有理数x,x′(x＜x′)について、a^x＜a^x′である。そして、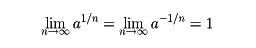

であるから、実数xに対して、r₁, r₂,……をxに収束する有理数の列とすれば、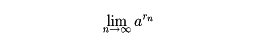

が存在して、この極限値はxのみによって定まり、xに収束する有理数列のとり方にはよらないことがわかる。この値をa^xと定める。このようにしてすべての実数xについてa^xが定められ、これについても指数法則は成立する。0＜a＜1のときはa^x＝(1/a)^-xと定めればよい。y＝a^xのグラフでは、a＞1のとき、a^xは増加関数で、x＝0のときy＝1となる。そして、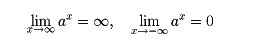

0＜a＜1のとき、a^xは減少関数で、x＝0のときy＝1、そして、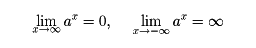

指数関数の底としては、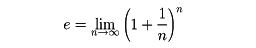

である数eを用いることが多い。これは無限級数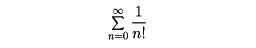

の和としても得られる。

　　e＝2.71828182845904523536……
これを用いると、

指数関数の微分、積分は次のようになる。

ここでlogaはaの自然対数である。

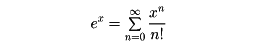
はxのすべての複素数値に対して収束する級数であるので、これによってe^xの、指数xを複素数に拡張したときの値を定義する。

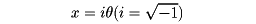
と置けば、
　　e^iθ＝cosθ＋isinθ
となる。これをオイラーの公式という。一般の
複素数α＋iβについては、
　　e^α+iβ＝e^α(cosβ＋isinβ)
となる。

　e^xはexpxと書くことも多い。指数関数の定義の仕方について述べておこう。解析教程の多くは、本文のように指数関数を定義したあとに、その逆関数として対数関数を定義して、それらの導関数や積分を調べていくことになっている。しかしながら、有理数の指数の定義（一般の正数についてm乗根の存在をあらかじめ証明しておかなければならない）から出発して実数の指数の定義にまで到達するのには、実数論特有の相当の手間がかかり、厳密な証明はやさしいものではない。一方、対数関数には、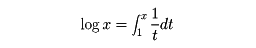

の関係がある。そこで直観的にわかりやすく定積分の議論をある程度済ませたあとで、この積分で逆に対数関数を定義する。こうしても論理的整合性の失われる部分は少ないし、対数関数の満たす関数方程式を、積分の知識から形式的に証明できる。したがって、この形で対数関数を導入して、その逆関数として指数関数を教えるほうがよいという意見も多く、しばしばこの方法が試みられている。

［竹之内脩］

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

指数関数 (しすうかんすう)
exponential function

正の数aの累乗aⁿ（aのn乗）を考えるとき，nを累乗の指数というが，指数の概念を任意の実数xに拡張しa^xを以下のように定義する。まず正の有理数r＝m/n（m，nは正の整数）に対して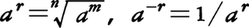と定義する。次に任意の実数xに対して，xに収束する有理数列｛r_n｝をとり

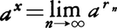と定義する。

　こうしてa^xがすべての実数xに対して定義されて，指数法則が成り立つ。

　さらに，a^xはxに関して連続的に変化する。すなわちa^xはxの連続関数である。a＝1のときはa^x≡1となるが，通常この場合を除外し，1に等しくない任意の正の定数aを与えたとき，実数全体を定義域とする関数，

　f（x）＝a^x　　……（1）　

をaを底とする指数関数という。a＞1ならばxが増加するに従ってa^xも単調に増加し，0＜a＜1ならばxが増加するに従ってa^xは単調に減少する。

　次の極限値の存在が知られている。

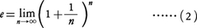
このeを自然対数の底という。eは円周率πと同様に数学でもっとも重要な定数の一つである。これは超越数であって，その十進小数展開の一部を書くと，

　e＝2.718281828459……

となる。またeは次の無限級数で表すこともできる。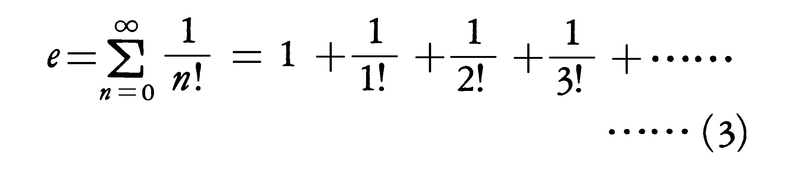

eを底とする指数関数，すなわち（1）においてa＝eとして得られる関数，

　f（x）＝e^x　　……（4）　

を，通常，単に指数関数といい，exp xとも書く。このときaを底とする指数関数はa^x＝e^{xlog a}と表される。指数関数（4）の導関数は，

　f′（x）＝f（x）　（すなわち（e^x）′＝e^x）　　……（5）　

を満たす。逆にf′（x）＝f（x）となる関数はe^xの定数倍に限る。また，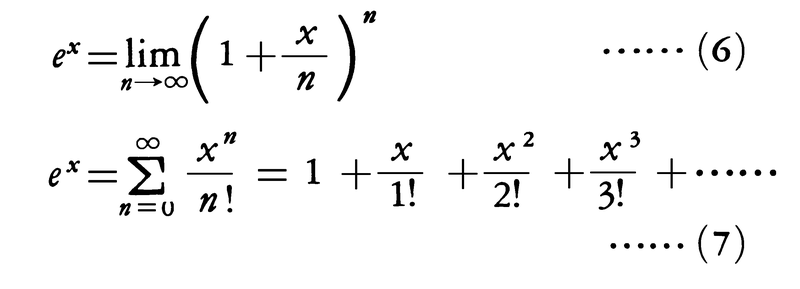

が成立するので，（6）の極限値または（7）のべき級数で指数関数e^xを定義してもよい。（7）のべき級数において実数xを複素数zで置き換えたものは，任意の複素数zに対して収束するので，この式によって複素変数の指数関数e^z（exp zとも書く）を定義する。この定義と三角関数cos z，sin zの定義とから，e^iz＝cos z＋i sin zが導かれる。ここでz＝iθ（θは実数）とした式，

　e^iθ＝cosθ＋i sin θ

をオイラーの公式という。この式により，複素数z＝x＋iy（x，yは実数）の指数関数e^z＝e^x⁺^iy＝e^xe^iyにおいて，e^xはe^zの絶対値，yはe^zの偏角を表すことがわかる。
→対数　→対数関数
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

指数関数
しすうかんすう
exponential function

ねずみ算などの倍増しの法則を定式化したもので，x を任意の実数とするとき，関数 y＝a^x(a＞0) を，a を底とする指数関数という。その逆関数を a を底とする対数関数という。指数関数の値は，常に正である。最も重要な指数関数は y＝e^x (または y＝ exp x ) である。ここで e は，ネーピアの数 (自然対数の底) であって
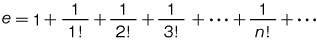で与えられる。指数関数 e^x は
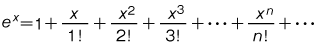のように，マクローリン級数に展開できる。また，これは，変数 x を複素数として複素変数の場合に拡張される。このべき級数は複素平面上のあらゆる点で収束し，特に実数値 x に対しては e の x 乗と等しくなる。この性質から，上記のべき級数で定義された解析関数を，e^x で表わし，これを指数関数という。複素数 z＝x＋iy と表わせば，

e^z＝e^x+iy＝e^x・e^iy＝e^x( cos y＋i sin y)

が成り立つ。指数関数 y＝e^x のグラフを指数曲線という。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

指数関数【しすうかんすう】

aを正の定数，xを実数の変数とする関数a(x/)をいう。特にe(x/)（eは自然対数の底）が重要で，この関数は何回微分または積分しても同じ形を保つ。一般の指数関数a(x/)はe(x/) (log/) (a/)と書ける。xが複素数の場合にも拡張できる。→指数／対数／自然対数
→関連項目双曲線関数

出典　株式会社平凡社