逆関数（読み）ギャクカンスウ（英語表記）inverse function

デジタル大辞泉

ぎゃく‐かんすう〔‐クワンスウ〕【逆関数】

関数y＝f （x）のxとyとを入れ換えて得られる関数x＝f （y）のこと。y＝f^－1（x）と表す。

出典　小学館

精選版 日本国語大辞典

ぎゃく‐かんすう‥クヮンスウ【逆関数】

1. 〘 名詞 〙
2. ① 関数の独立変数と従属変数の役割を入れ換えて得られる関数の、もとの関数に対する称。y=2x-4 に対する y=½x+2 など。
3. ② 全単射である関数の逆写像。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

逆関数 (ぎゃくかんすう)
inverse function

xの関数y＝f（x）があるとき，その値域に属するyのおのおのの値に対して，y＝f（x）となるxがただ一つ定まる場合，xをyの関数と考えてx＝f⁻¹（y）と書き，f⁻¹をfの逆関数という。例えばf（x）＝\(\sqrt{x}\)の逆関数はf⁻¹（x）＝x²である。fの定義域，値域ともに実数の集合の場合は，fが狭義単調（fにおいてx₁＜x₂ならば，f（x₁）＜f（x₂），またはf（x₁）＞f（x₂）が成り立つ）ならば逆関数f⁻¹が存在する。同じ直交座標系に関して，y＝f（x）のグラフとy＝f⁻¹（x）のグラフとは，直線y＝xに関して対称である。

　なお，yの値に対してy＝f（x）となるxの値がただ一つでない場合，すなわちxがyの多価関数となる場合も，その多価関数をもとの関数fの逆関数という。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

逆関数
ぎゃくかんすう
inverse function

逆写像 inverse mappingともいう。 A から B への関数 f が全単射のときは，y∈B について f(x)＝y となる x∈A が定まるわけなので，y にこの x を対応させることによって，B から A への関数 x＝g(y) が定まる。この g を f の逆関数という。一般の関数の場合には，y∈f(A) について，f(x)＝y となる x があるが，これが一意的とかぎらないので，y から x を対応させようとしても，多価関数になってしまう。この場合には，リーマン面のようなものを考えて，f(A) のほうを何重かにして一価関数としての逆関数が考えられるようにするか，初等的には f の定義域を制限しておくなどする。たとえば，実数 R から R への関数 y＝x² では f(R) は正の半直線 R₊ ，その範囲でも x は ±√y の2つがあるが，定義域を R₊ に制限すると，R₊ から R₊ への全単射が得られるので，逆関数 x＝√y が得られる。 ±√y の出てくる逆関数を考えるには，R₊ を2重にして，つまり直線を2つ折りにした空間を考えると，そこから R への関数と考えることができる。

出典　ブリタニカ国際大百科事典 小項目事典

日本大百科全書(ニッポニカ)

逆関数
ぎゃくかんすう
inverse function

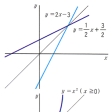
ある数yが、他の数xの変化に伴って変化するとき、yをxの関数といい、y＝f(x)で表す。この逆向きの対応を考えて、y＝f(x)の関係があり、その値域に属するyの変化に伴って、xの値がただ一つ定まるとき、これを逆関数という。y＝f(x)の逆関数はx＝f^-1(y)で表す。一般にy＝f(x)の逆関数を求めるには、これをxについて解いてx＝g(y)の形とし、ここでxとyを入れ替える。こうして、逆関数y＝g(x)が定まる。たとえば、y＝2x－3の逆関数を求めるには、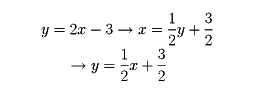

とすればよい。同様に、定義域をx≧0とした場合のy＝x²の逆関数は、y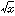＝であり、指数関数y＝a^x(a＞0, a≠1)の逆関数は、対数関数y＝log_axである。y＝f(x)のグラフとy＝f^-1(x)のグラフは、直線y＝xに関して互いに対称である。

［竹之内脩］

逆関数のグラフ

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

逆関数【ぎゃくかんすう】

xの関数y＝f（x）において，その値域に属するyの各値に対し対応するxの値が定まるとき，xをyの関数とみなしx＝f(-/)¹（y）と書き，これをもとの関数f（x）の逆関数という。普通は変数をx，関数をyと書くので，逆関数の表現はy＝f(-/)¹（x）となる。たとえばf（x）＝a(x/)（a＞０）ならば，f(-/)¹（x）＝log(/a)x。→逆三角関数
→関連項目写像

出典　株式会社平凡社