極大・極小 (きょくだいきょくしょう)
relative maximum, relative minimum
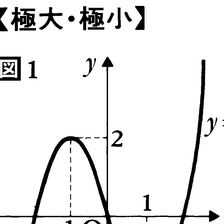
点cを含む一つの集合Eで定義された実数値関数f(x)があるとする。cに十分近いEのすべての点でf(x)≦f(c)となるとき,fはcにおいて極大となる,あるいは極大値f(c)をとるという。cに十分近いEのすべての点でf(x)≧f(c)となるとき,fはcにおいて極小となる,あるいは極小値f(c)をとるという。いいかえるとf(c)が極大値であるというのは,cの近くでだけ(すなわち局所的に)考えたときの最大値であって定義域全体で考えたときの最大値とは限らない。極小値についても同様である。例えば,Eを実数全体とするとき,f(x)=x2についてはf(0)=0は極小値で,同時に最小値でもある。しかし図1で示すようにf(x)=x3-3xについてはf(-1)=2は極大値ではあるが最大値でなく,f(1)=-2は極小値ではあるが最小値でない。極大値と極小値とを総称して極値という。
f(x)が実数のある区間で定義された微分可能な関数であって,cをその区間の内部の1点とする。このとき,(1)fがcにおいて極値をとるならばf′(c)=0である。(2)cに十分近いところでx<cにおいてf′(x)>0で,x>cにおいてf′(x)<0となるなら,f(c)は極大値である。f′(x)に関する不等号の向きがこれと逆の場合はf(c)は極小値である。(3)fが2回微分可能であってf′(c)=0のときは,f″(c)<0ならf(c)は極大値,f″(c)>0ならf(c)は極小値である。なお,(1)の逆は成り立たない。すなわち図2の例のようにf′(c)=0でもf(c)は極値とは限らない。
執筆者:伊藤 清三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
Sponserd by 
極大・極小
きょくだい・きょくしょう
maximal and minimal
関数 f(x) が,定義域 D の内点 a のある近傍において局所的に最大あるいは最小になるとき,f(x) は極大あるいは極小になるといい,そのときの値 f(a) を極大値あるいは極小値という。これを正確に述べれば次のようになる。すなわち,ある正の数 δ が存在して,0<|x-a|<δ ならば f(x)-f(a)<0 あるいは f(x)-f(a)>0 が成り立つとき,f(x) は点 a で極大あるいは極小である。またこの a を f(x) の極大点あるいは極小点ということがある。極大値,極小値を合せて極値という。 f(x) が点 a∈D で微分可能なとき,f(x) が x=a で極値をとるためには,f'(a)=0 となることが必要である (必要条件) 。これは十分条件ではない。たとえば f(x)=x3+1 は,x=0 のとき f'(0)=0 であるが,f(0) は極大値にも極小値でもない。 f(x) が点 a∈D の近傍で微分可能かつ f'(a)=0 で,もし f'(x) が a を通過するとき,その符号を+から-に,あるいは-から+に変えるならば,f(a) は極大値あるいは極小値となる (十分条件) 。一般に,f(x) が点 a∈D の近傍で n-1 回微分可能であり,a で n 回微分可能であって,f'(a)=f''(a)=…=f(n-1)(a)=0 かつ f(n)(a)≠0 のとき,(1) n が偶数で,f(n)(a)<0 ならば f(a) は極大値,f(n)(a)>0 ならば f(a) は極小値となる。 (2) n が奇数ならば f(a) は極値とならない。
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
Sponserd by 
極大・極小【きょくだい・きょくしょう】
x=aを含む範囲で定義された関数y=f(x)がaに十分近いすべての点xでf(x)≦f(a)(f(x)≧f(a))となるならば,f(x)はx=aで極大(極小)であるといい,f(a)を極大(極小)値という。極大・極小値を合わせて極値という。f(x)が微分可能ならばf′(a)=0でf″(a)<0(>0)のときf(x)はx=aで極大(極小)。→変曲点
→関連項目変分学
出典 株式会社平凡社百科事典マイペディアについて 情報
Sponserd by