画法幾何学（読み）ガホウキカガク（その他表記）descriptive geometry

デジタル大辞泉

がほう‐きかがく〔グワハフ‐〕【画法幾何学】

空間図形を平面上に表す方法を論ずる幾何学の一部門。投影図法を用いたG＝モンジュが創始者とされる。

出典　小学館

精選版 日本国語大辞典

がほう‐きかがくグヮハフ‥【画法幾何学】

1. 〘 名詞 〙 幾何学の一分科。空間の図形を平面図形によって正確に表わす方法を研究する学問。一八世紀フランスのモンジュが創始。構造物や機械の設計などに応用される。〔工学字彙（1886）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

画法幾何学 (がほうきかがく)
descriptive geometry

三次元の空間図形（点，線，面ならびにこれらで構成されている立体）を，二次元の平面上に表示し，かつこれらの図形の相互関係を定性的，定量的に考察する学問で，分類上は幾何学の一分野。図法幾何学，立体図学とも呼ばれる。画法幾何学の創始者はフランスのG.モンジュで，彼は城壁の設計を計算によらず作図によって解く方法を開発した。この図式解法は当初は軍事機密とされたが，のちに公開が認められた。1799年に出版された彼の著書《Géométrie descriptive》が以後画法幾何学の原典になり，いちはやく各国の軍事関係の学校で学習され，その後は工業製図の分野に大きな影響を及ぼした。

投影法とその種類

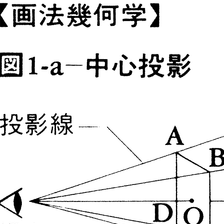
ある物体（空間図形）を一つの集合と考えたとき，いまその1点Aをとりあげて，これを物体の先方に置いた平面Pに見通せば，P上にはこれに対応する点A′を印することができる。このような操作を投影projectionまたは投象といい，平面Pを投影面と呼ぶ。同様にして物体の各点を次々に投影していけば，平面上にはその物体の対応図形が得られ，こうして得られた図形を投影図，視点と投影図を結ぶ直線を投影線という。視点が投影面から有限な距離にあるときは，投影線はすべて視点という1点（投影中心）に集中するが，この投影中心が投影面から無限に遠ざかれば，図形のすべての点を通る投影線は互いに平行となる。前者を中心投影（または透視投影）といい，後者を平行投影という。このうち平行投影は，投影面と投影線が互いに直角であるか否かによって，垂直投影と斜投影に分類され，垂直投影はさらに正投影，軸測投影，標高投影に分けられる。（1）正投影　垂直投影のうち，物体の直交座標軸がそれぞれ投影面に平行あるいは直交しているとき（図2-a）。この投影法では，一つの投影面には物体の1面しか投影することができないので，図2-bのように，互いに直交する投影面V，Hを設け，それぞれの面に垂直な投影線によって投影したのち，二つの投影面の交わる線（基線という）を軸として，矢印で示す方向に90°回転させて1平面上に置いて表す。このとき物体が，二つの投影面のつくる第1～第4象限のいずれに置かれるかによって，図2-bに示すような配置が得られるが，これらをそれぞれ第一～第四角法と名づける。このうち第一角法と第三角法では，図形の配置がそれぞれ逆になる。また第二角法と第四角法は，投影後に投影面を回転させたとき，両方の投影した図形が重なり合って見にくいので採用されない。このように正投影は，一般に複数の投影面を必要とするので，複面投影とも呼ばれる。これに対し，以下に説明する投影法は，1個の投影面によって物体の形状を表現することができるので，単面投影とも呼ばれており，いわゆる立体図がこれである。（2）斜投影　平行投影のうち，投影面に対してある角度をもった投影線によって投影を行うもの。一般には物体の位置を，正投影の場合と同じく，その直交座標軸が投影面に平行あるいは直交するように置いて投影を行う場合が多く，このときには物体の正面は正投影の場合とまったく同じように表される（図3）。（3）軸測投影垂直投影のうち，物体の直交座標軸がいずれも投影面に交わるように傾けて置かれたとき（図4）。投影図における座標軸がそれぞれ120°で交わる場合を等軸測投影，それ以外の角度で交わる場合を不等軸測投影という。（4）中心投影　投影中心から発散する投影線によって投影する場合（図5）。投影中心の数により1点透視，2点透視などのものがある。実際に目で見た場合と同様に，きわめて自然に描き表せることから建築物の完成予想図などに利用される。（5）標高投影　物体をある基準面からの高さで表現する場合で，地表のような凹凸のある複雑な面を，一般に水平線から等しい高さにある点を結ぶいわゆる標高線で表したもの（図6）。
執筆者：大西 清

図1～図6

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

画法幾何学
がほうきかがく

三次元、すなわち長さと幅と高さをもつ空間図形を、二次元、すなわち長さと幅しかもたない平面上に表し、その形、大きさ、位置などを研究する幾何学の一部門をいう。投影図法および透視図法がもっともよく知られ、また、もっとも重要な方法である。

　投影図法は、空間図形を、互いに垂直に交わる二つの平面上への正射影を一つの平面に描いて、これをもとの空間図形にかえる方法であり、透視図法（中心投影法ともいう）は、空間図形を、有限距離にある一点を中心として一平面上に射影し、これをもとの空間図形にかえる方法である。

　投影図法は18世紀の末ごろフランスのモンジュによって始められたもので、モンジュを画法幾何学の創始者とする人が多い。また、透視図法は、デザルグ、パスカルらの考えに端を発しているが、いわゆる近世幾何学への道を開き、ポンスレらによって総括されて射影幾何学へと発展した。

［矢野健太郎］

[参照項目] | 射影幾何学

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

画法幾何学
がほうきかがく
descriptive geometry

3次元空間，すなわち普通の空間内の立体について，点，直線，平面あるいはその他の曲面の位置や形の関係を研究する幾何学の一分野である。画法幾何学は，建築工学や機械工学上のあらゆる問題に，基礎的な理論づけを与えるもので，3次元空間における立体を2次元空間すなわち平面上にかくことによって，問題を解決する有効な方法となる。そこで用いられる方法は，正射影法であるが，透視図法も利用される。また使用される概念は，平面幾何学や立体幾何学の公理や定理に基礎づけられたものである。画法幾何学は，フランスの数学者 G.モンジュによって創始された。現在の画法幾何学は，正射影法や透視図法ばかりでなく，斜投影法や軸測投影法など，種々の画法が研究対象となっている。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

画法幾何学【がほうきかがく】

→立体図学

出典　株式会社平凡社

世界大百科事典（旧版）内の画法幾何学の言及

【製図】より

…その後，印刷術の発明により，機械を写した図，書物は多数を数えることになるが，その中でG.アグリコラによる《デ･レ･メタリカ》はとくに著名である。　近世に入って，G.モンジュによって創始された画法幾何学は，築城の技術に一大躍進をもたらした。それまでめんどうな計算を行って解かなければならなかった問題が，作図により容易に解決できるようになったのである。…

※「画法幾何学」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」