絶対不等式（読み）ぜったいふとうしき（英語表記）absolute inequality

改訂新版　世界大百科事典

絶対不等式 (ぜったいふとうしき)
absolute inequality

不等式a²＋b²＋c²≧bc＋ca＋abは，文字a，b，cがどのような実数であっても成り立つが，不等式x²－3x＋2＜0は1＜x＜2なる範囲のxについてのみ成り立つ。第1の例のように，その中に含まれる文字にどのような実数値を与えても成り立つ不等式を絶対不等式といい，第2の例のように，その中に含まれる文字が限定されたある範囲に属するときにのみ成り立つ不等式を条件付不等式（条件不等式ともいう）という。しかし，文字を変数と考えるとき，a≧0，b≧0のように十分一般的な変域において成り立つ不等式は，絶対不等式と呼ぶ。例えば，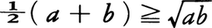

はa≧0，b≧0として成り立つ絶対不等式と考える。これは二つの負でない実数の相加平均は相乗平均より小さくないことを表しているが，一般に，n個の正の実数の間にも，

　相加平均≧相乗平均≧調和平均

という絶対不等式が成り立つ。すなわち，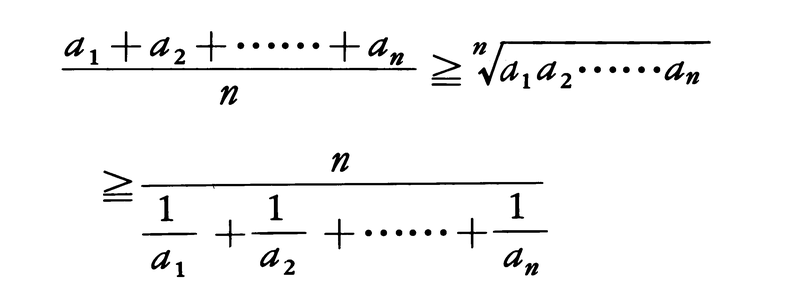

等号はa₁＝a₂＝……＝a_nのときに成立する。

　いくつかの重要な絶対不等式の例をあげる。平面上の二つのベクトルa＝（a₁，a₂），b＝（b₁，b₂）のなす角をθとすると，cosθ＝（a，b）/｜a｜・｜b｜（分子はベクトルの内積，分母はベクトルの長さの積）だから，｜cosθ｜≦1なることにより次の不等式が得られる。

　（a₁b₁＋a₂b₂）²≦（a₁²＋a₂²）（b₁²＋b₂²）

n次元のベクトルについても，同様にして，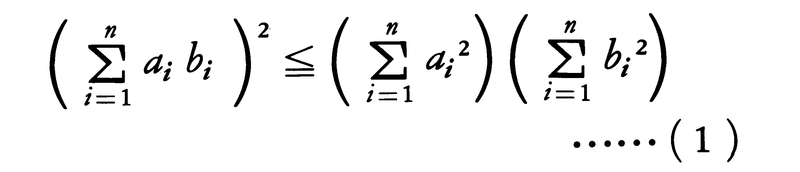

これをコーシー=シュワルツの不等式という。また，ベクトルの長さに関してよく知られた関係｜a＋b｜≦｜a｜＋｜b｜を成分で表したものをn次元のベクトルについて書けば，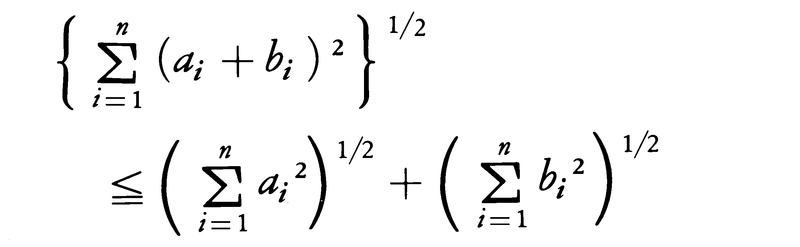

さらに一般に，任意のp≧1に対して，不等式，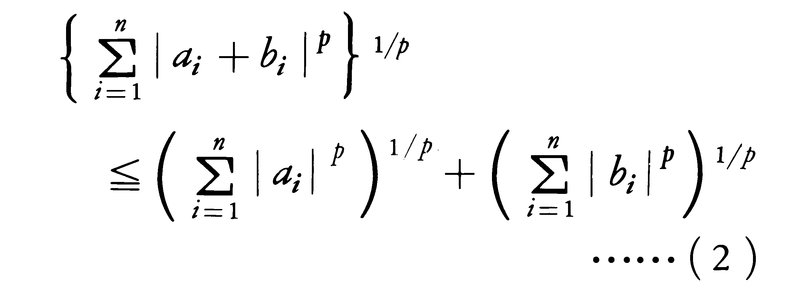

が成立する。これをミンコフスキーの不等式という（0＜p＜1のときは逆向きの不等式が成立する）。（1），（2）において等号が成立するのはa_iとb_iとが比例するときである。（1）と（2）を積分可能な関数f（x），g（x）に拡張した次の（1′），（2′）もそれぞれシュワルツの不等式，ミンコフスキーの不等式と呼ばれる。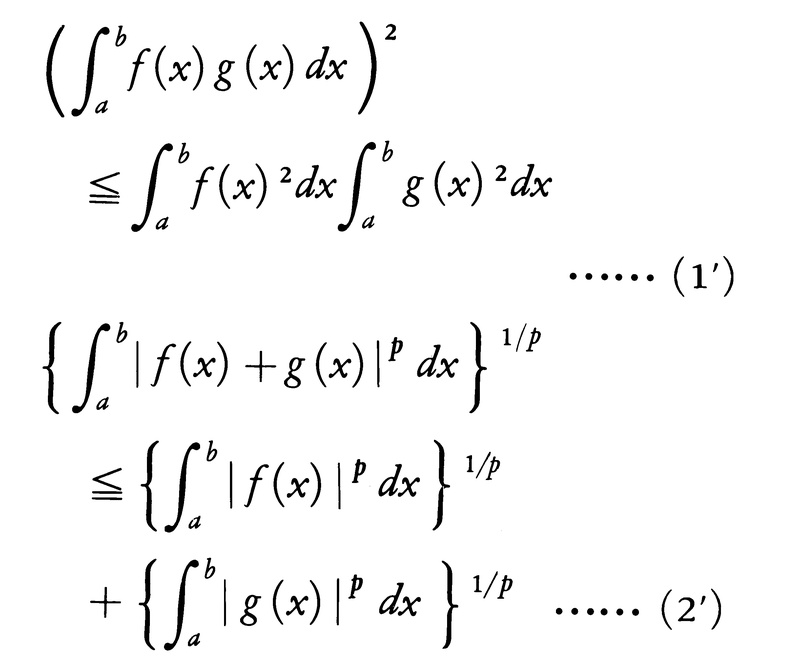

　以上のほか，行列式D＝det（a_ij）に関する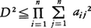，　……（アダマールの定理）　

も有名な絶対不等式である。
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

絶対不等式
ぜったいふとうしき
absolute inequality

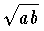不等式に含まれる文字が，どのような値をとっても成り立つような不等式をいう。 x²＋3x＋4＞0 ，x²＋y²＋2＞0 などは絶対不等式である。よく知られている絶対不等式に，a＞0 ，b＞0 のときの，算術平均 (a＋b)/2 ，幾何平均 ，調和平均 2ab/(a＋b) の間の関係式，算術平均 ≧ 幾何平均 ≧ 調和平均 (等式が成り立つのは a＝b に限る) やシュワルツの不等式がある。絶対不等式に対して条件つき不等式がある。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の絶対不等式の言及

【不等式】より

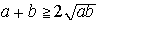…a≧b＞0,c≧d＞0ならばac≧bdなどのような不等式の基本的性質は，すべて(1)，(2)から導かれる。　文字a,b，……に関する不等式が，それらの文字にあらかじめ定められた範囲の値を与えたときつねに成立する場合に，その不等式を絶対不等式という。a²≧0はすべての実数aに対して成立し，はすべての正数a,bに対して成立する絶対不等式である。…

※「絶対不等式」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」