逆三角関数（読み）ギャクサンカクカンスウ

デジタル大辞泉

ぎゃく‐さんかくかんすう〔‐サンカククワンスウ〕【逆三角関数】

三角関数の逆関数。例えば、正弦関係y＝sinxの逆関数はsiny＝xで、これをy＝sin^－1xまたは、y＝arcsinxと書き、アークサインxと読む。

出典　小学館

精選版 日本国語大辞典

ぎゃく‐さんかくかんすう‥サンカククヮンスウ【逆三角関数】

1. 〘 名詞 〙 三角関数の逆関数。逆正弦、逆余弦、逆正接、逆余接、逆正割、逆余割関数の総称。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

逆三角関数
ぎゃくさんかくかんすう

三角関数の逆関数の総称。三角関数は、たとえばy＝sinxにおいてsin30゜, sin45゜, sin60゜,…のようにxの変化に伴うyの値を求めることになるが、逆三角関数は、この逆にsinx＝aにおいてaの値が1/2, 1/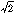, 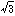/2……と変化するときのxの値（角）を求める。三角関数の正弦、余弦、正接のそれぞれに対応する逆三角関数があるが、ここでは、逆正弦関数、逆余弦関数、逆正接関数の三つについて考えることにする。なお、逆三角関数の考察が重要となるのは、微分積分法においてであるので、その意味で角は弧度法（ラジアン）を用いる。

(1)逆正弦関数　sinxは－1から1までの間の値をとる。逆関数を考える場合は、この関数が1対1であるような範囲に制限して定義域をとらねばならない。そのための区間として
　　－π/2≦x≦π/2
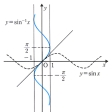
をとる。この区間内でsinxは－1から1まで増加する。したがって、－1≦b≦1を満たすbに対して、b＝sinaを満たすようなaがただ一つ定まる。これをbに対応させることによって、逆関数a＝sin^-1b（sin^-1bは、インバース・サインbと読む）が定まる。y＝sin^-1xのグラフはy＝sinxのグラフを直線y＝xに関して対称に折り返したものである（図A）。y＝sin^-1xは－1≦x≦1において定義された－π/2からπ/2まで増加する連続関数である。それは微分可能で、導関数は、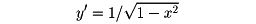

である。b＝sinxを満たす一般のxの値は
　　x＝nπ＋(－1)ⁿsin^-1b
　　　(n＝0,±1,±2,……)
で与えられる。

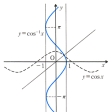
(2)逆余弦関数　cosxの定義域を0≦x≦πで考えると、この関数はこの区間内で1から－1まで減少する。したがって－1≦x≦1を定義域とする逆関数y＝cos^-1xが得られる。y＝cos^-1xは－1≦x≦1において定義されたπから0まで減少する連続関数である（図B）。それは微分可能で、導関数は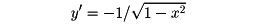

である。b＝cosxを満たす一般のxの値は
　　x＝2nπ±cos^-1b
　　　(n＝0,±1,±2,……)
で与えられる。また、sin^-1x＋cos^-1x＝π/2である。

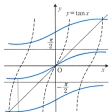
(3)逆正接関数　tanxは－π/2＜x＜π/2においてすべての実数値をとる増加関数である。ゆえに、逆関数y＝tan^-1xは、すべての実数値に対して定義された－π/2からπ/2まで増加する連続関数である（図C）。それは微分可能で、導関数はy′＝1/(1＋x²)である。b＝tanxを満たす一般のxの値は、
　　x＝nπ＋tan^-1b (n＝0,±1,±2,……)
で与えられる。

［竹之内脩］

逆正弦関数〔図A〕

逆余弦関数〔図B〕

逆正接関数〔図C〕

おもな逆三角関数の値

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

逆三角関数 (ぎゃくさんかくかんすう)
inverse trigonometric function

正弦関数y＝sin xの値域は区間［－1，1］である。この区間に属する任意のyに対してsin x＝yとなるxは無数にあるが，xの変域を［－π/2，π/2］に制限すると，このようなxはただ一つ定まる。このとき，

　x＝Arcsin y，またはx＝Sin⁻¹y

と書き，この関数y→xを逆正弦関数という。すなわちx＝Arcsin yは，－π/2≦x≦π/2を定義域とする正弦関数y＝sin xの逆関数である。同様にして，0≦x≦πを定義域とする余弦関数y＝cos xの逆関数を，

　x＝Arccos y，またはx＝Cos⁻¹y

と書き逆余弦関数という。また，－π/2＜x＜π/2を定義域とする正接関数y＝tan xの逆関数を，逆正接関数と呼んで，

　x＝Arctan y，またはx＝Tan⁻¹y

と書き，0＜x＜πを定義域とする余接関数y＝cot xの逆関数を，逆余接関数と呼んで，

　x＝Arccot y，またはx＝Cot⁻¹y

と書く。sec x，cosec xの逆関数も同様にして定義されるが，これらはたいして有用でない。以上に述べた6個の三角関数の逆関数を総称して逆三角関数という。

　正弦関数y＝sin xの定義域を制限しない場合は，その逆関数を考えると多価関数になる。それを逆正弦関数と呼んで，

　x＝arcsin y，またはx＝sin⁻¹y

と書くこともある。この場合には，前に述べたArcsin yを逆正弦関数の主値という。逆余弦関数arctan y（cos⁻¹y），逆正接関数arctan y（tan⁻¹y）など，およびそれらの主値という言葉も，同様に定義される。逆三角関数という名称は，これらの多価関数を指すこともある（図）。

　以上の記述においては，三角関数の逆関数として説明したため，逆三角関数の独立変数をyで表したが，最初から逆三角関数を扱うときにはもちろん独立変数をxと書いてよい。例えば逆正弦関数はy＝arcsin x，またはsin⁻¹x（主値ならばArcsin x，Sin⁻¹x）のように書く。逆余弦関数，逆正接関数についても同様である。逆三角関数（主値）の微分法については，次の公式が成り立つ。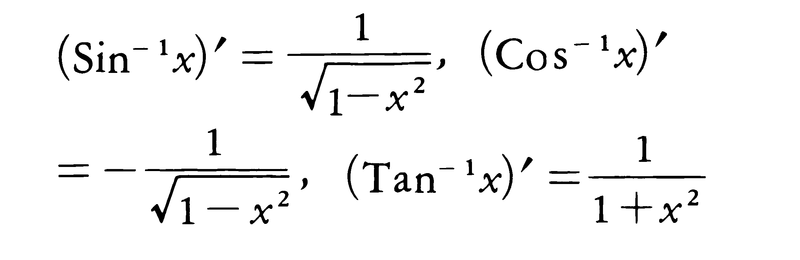


執筆者：伊藤 清三

図－逆三角関数

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

逆三角関数
ぎゃくさんかくかんすう
inverse trigonometric function

三角関数の逆関数をいい，y＝ arcsin x，arccos x，arctan x，arccotx などで表わす。たとえば，－1≦y≦1 のとき，y に対して y＝ sin x となる x を対応させる関数と x＝ arcsin y は同義である。三角関数は，周期関数で同じ値を無限に多くとるから，逆三角関数は無限多価関数である。しかし三角関数のグラフからわかるように，たとえば y＝ sin x は －π/2≦x≦π/2 で強い意味の単調増加関数であり，区間 －1≦y≦1 内の任意の値を1回ずつとるので，その逆関数 y＝ arcsin x は，値を －π/2≦y≦π/2 とすれば，－1≦x≦1 で一価関数となる。こうして得られた一価関数 y を arcsin x の主値という。各逆三角関数 y が主値をとる区間は次のとおりである。
y＝ arcsin x，arccos x，arctan x のグラフは，図のようになる。太い線の部分が，一価関数として考えられた y のグラフである。なお arcsin x を sin ^-1x などと表わすこともある。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

逆三角関数【ぎゃくさんかくかんすう】

三角関数の逆関数。sin x，cos x，tan x等の逆関数をarcsin x，arccos x，arctan x等（またはsin(-/)¹x等）と書く。たとえばarcsin1はsin x＝１となるxの値で，（π/2）＋２nπ（nは整数）。逆三角関数は無限多価関数。→関数

出典　株式会社平凡社