限界生産力（読み）げんかいせいさんりょく（英語表記）marginal productivity

日本大百科全書(ニッポニカ)

限界生産力
げんかいせいさんりょく
marginal productivity

他の生産要素の投入量が不変であるときに、特定の生産要素の投入量をある水準から1単位増やすことにより得られる生産物の増加分のこと。一般に限界生産力は、生産要素投入量の増加とともに減少する傾向がみられ、これを限界生産力逓減(ていげん)の法則という。

　いま生産量をY、労働投入量をLとすると、生産関数は
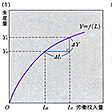
　　Y＝f(L)
と表される。図の(1)に示されているように、労働投入量がL₀からL₁へと増加すると、生産量はY₀からY₁へと増える。

　　ΔL＝L₁－L₀，ΔY＝Y₁－Y₀
とすると、労働投入ΔL単位の増加に対し、生産量はΔYだけ増えたのであるから、このときの労働の限界生産力は、ΔY/ΔLで示される。労働投入の増え分を無限に小さくしていくと、結局生産関数の傾きが労働の限界生産力を示すことになる。図の(1)のような生産関数では、労働投入量が増えていくと生産関数の傾きはしだいに緩やかになる。これが労働の限界生産力逓減の法則である。

　次に、貨幣賃金率w、生産物価格pが所与であるときの企業の労働投入決定の仕方を考えてみよう。企業の収入はpY＝pf(L)であり、労働費用はwLである。図の(2)において、利潤（＝pY－wL）は収入曲線pYと労働費用直線wLとの垂直距離として示される。企業はこの利潤が最大となる労働投入量を選択する。それは直観的に明らかなように、収入曲線の傾きと労働費用直線の傾きとが等しくなる労働投入量である。つまりこのとき、労働の価値限界生産力（労働の限界生産力と生産物価格との積）は貨幣賃金率に等しい。これはまた、実質賃金率（w/p）と労働の限界生産力との均等と読み替えることができる。労働の価値限界生産力が貨幣賃金率よりも大きい（小さい）ならば、労働雇用を追加（削減）することにより、利潤を高めることができる。

　このような限界生産力概念は、生産理論、分配理論において重要な役割を果たしている。

［内島敏之］

[参照項目] | 限界生産力説 | 生産関数

限界生産力説明図〔図〕

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

限界生産力 (げんかいせいさんりょく)
marginal productivity

ある財の生産を行っているときに，一つの生産要素だけを1単位増加させたときの生産物の増加量を限界生産力（または生産性）と呼ぶ。したがって限界生産力は，その生産物を生産するにあたって，その生産要素が（限界的に）どの程度有効であるかを表す指標である。ある一定の大きさの土地で米を作るとき，散布する肥料の量を考えてみると，散布量の少ないときに肥料を1単位（たとえば1kg）増やしたときの限界生産力は，すでに大量の肥料を散布したときの追加的1単位の限界生産力に比べて大きいと考えられる。つまり限界生産力は，その投入物の投入量を増やすにしたがって逓減する。これを〈限界生産力逓減の法則〉という。
執筆者：奥野 正寛

出典　株式会社平凡社「改訂新版　世界大百科事典」

栄養・生化学辞典

限界生産力

　生産のための要素が単位量増加したときの効果を数量化したもの．

出典　朝倉書店

世界大百科事典（旧版）内の限界生産力の言及

【限界生産力説】より

…労働，土地，資本などの生産要素を使用して生産物を生産するとき，他の生産要素の量を一定にして，ある生産要素をもう1単位だけ増加することにより可能になる生産物の量の増加を，その生産要素の〈限界生産力〉とよぶ。そして，生産物は賃金，地代，利潤などのかたちで生産要素に分配されるが，それはそれぞれの生産要素の限界生産力によって決定されるという分配理論が，限界生産力説である。…

※「限界生産力」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」