数量化（読み）すうりょうか

改訂新版　世界大百科事典

数量化 (すうりょうか)

ある現象を解明するためには，調査対象をいくつかの側面から同時に測定した多変量データの分析が重要である。測定値には数量で与えられる量的データと数量では表現できない質的データとがあり，後者の方が扱いは難しい。数量化は質的な多変量データから有効な情報を引き出すために工夫された統計的データ解析法で，文部省統計数理研究所の林知己夫（ちきお）によって開発された。〈林の数量化〉〈（林の）数量化理論〉ともいい，数量化第Ⅰ類，第Ⅱ類，第Ⅲ類，第Ⅳ類と名づけられた四つの分析法を中核とする。これらは第Ⅱ類をさきがけとして1947年から55年にかけて基礎づけられた。いずれの方法も，（1）分析目的に合った統計量の構成，（2）統計量の最適化による質的な尺度から量的な尺度への変換，（3）変換された量の関係による質的なデータの構造の推定，という手続きをとる。数量化ということばは，質的な尺度を数量に変換することに由来する。コンピューターの発達により数量化の計算が容易になり，言語学，心理学，政治学，社会学，経営学，生態学，生物学，医学，情報科学など人文，社会，自然科学にわたる広い分野で利用される。

　質的データには2種類ある。一つは，たとえば個人の好みのように〈大好き〉〈好き〉〈好きでも嫌いでもない〉〈嫌い〉〈大嫌い〉といった，程度によって順序づけられるもので，順序尺度という。他の一つは，性別のように対象が属性を備えているか否かを示す名義尺度である。数量化では，順序尺度や名義尺度で記述される質的な要因をアイテムといい，その選択肢をカテゴリーという（たとえば上例では〈性別〉がアイテム，〈男〉〈女〉がカテゴリーである）。こうすれば，調査対象をアイテムごとに必ずあるカテゴリーに該当するようにできる。アイテムjのカテゴリーkに数量x_jkが与えられたとしよう。調査対象iの該当カテゴリーの数量をすべて取り出し，和y_iを作る。つまり，対象iがアイテムjのカテゴリーkに該当しているとき1，していないとき0となる記号n_ijkを導入すれば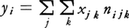，と表現できる。分析目的によってx_jkの定め方は異なり，第Ⅰ類から第Ⅳ類までの方法に分かれる。

数量化第Ⅰ類

調査対象iに一つの数量z_iが与えられている。zの変動を複数個の質的な要因で説明しようとする方法が第Ⅰ類である。カテゴリーの数量x_jkを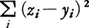，が最小になるように定める。これはz_iとy_iとができるだけ近づくことを意味する。その近さの程度はzとyとの相関係数値で評価される。計算手続きは，やや工夫がいるが重回帰分析（回帰分析）と一致し，x_jkは偏回帰係数に相当する。数量化の結果，zの変動にどのアイテムが影響しているか知ることができる。また相関係数値がかなり高いときには，新しい対象についてyを計算すればそれをzの予測値とみなすこともできる。応用例として，日本人の読み書き能力テストの正解得点を〈性別〉〈年齢〉〈学歴〉〈職業〉などのアイテムとそのカテゴリーから推定する試みや，テレビ視聴率の予測などがある。

数量化第Ⅱ類

対象iが複数個の群のいずれかに分類されているものとする。このとき質的な要因が群の離れぐあいにどれだけ影響を与えているか探る方法が第Ⅱ類である。x_jkを，同じ群に分類されている対象のyどうしは近い値をとり，異なる群に分類されている対象のyどうしは離れた値をとるように定める。統計的には相関比（群の離れぐあいを示す量）の2乗が最大になるようにx_jkを定めることに相当する。計算手続きは判別分析に一致し，固有値問題に帰着される。数量化の結果，分類に影響を与えているアイテムを知ることができる。また新しい対象についてyを計算し，どの群の値に近いかをみれば，その対象の属する群の予想もできる。第Ⅱ類を生み出すきっかけとなったのは，戦後間もない仮釈放の研究であった。仮釈放後1年以内に罪を犯した受刑者群とそうでなかった受刑者群とに分けて，受刑者の〈服役中の態度〉〈経歴〉〈社会復帰後の環境〉〈人格特性〉などからどちらの群である可能性が高いか調べられた。

　数量化第Ⅰ類と第Ⅱ類ではそれぞれ数量，分類といった分析目的となる情報が与えられている。この情報のことを外的基準という。第Ⅰ類，第Ⅱ類をそれぞれ〈外的基準が数量である場合の数量化〉〈分類である場合の数量化〉という。外的基準がない場合の数量化として第Ⅲ類と第Ⅳ類とがある。

数量化第Ⅲ類

対象iが性質jをもてば1，もたなければ0とすると，0と1のパターンが得られる。このパターンのみを手がかりにデータに隠れている構造を探り出す方法が第Ⅲ類である。パターン分類の数量化ともいう。対象iにu_i，性質jにv_jの数量を与える。対象どうしの0，1のパターンが似ていればuも近い値どうしになり，性質どうしのパターンが似ていればvも近い値になるようにする。統計的にはuとvとの相関係数が最大になるようにu_i，v_jをそれぞれ定めることに相当し，固有値問題になる。u，vの値によって対象群，性質群を分類し，どの対象群がどの性質群を共有しているかというその関連を調べることができる。u，vはそれぞれ一次元の量的尺度を構成していると考えられ，構成の程度を相関係数の大きさで評価する。第Ⅲ類はアイテム・カテゴリーあるいは度数で表現されたデータに適用してもよい。この方法は，被験者が缶詰のレッテルを好むか好まないかの嗜好（しこう）パターンにより被験者群とレッテル群とを同時分類する試みから考案された。

数量化第Ⅳ類

n個の対象のうち，2対象iとjとの類似度を表す数量e_ijのみが与えられている（e_ijは正で値が大きいほど似ているものとする）。対象i，jにそれぞれ数量w_i，w_jを与えて，e_ijが大のときは（w_i－w_j）²が小，反対にe_ijが小のときは大となるようにwを定める。統計的には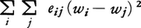がwの分散一定のもとで最小になるようwを定めることに相当し，固有値問題になる。このように対象間の関係の近さe_ijを平方距離（w_i－w_j）²におきかえて，n個の対象群の構造を視察しやすくする方法が第Ⅳ類であり，多次元尺度構成法の考え方に近い。集団の人間関係を成員間の親密さの程度から構造化する試みなどに利用される。

数量化の手順

数量化においては，（1）分析目的の明確化，（2）データの収集と編集，（3）分析法の適用，（4）結果の解釈と結論，の各段階が重視される。とくにアイテム，カテゴリーの選定は現象解明の決め手になる。数量化の結果からあらためてアイテム，カテゴリーを選び直し，ふたたび数量化を行う反復試行も必要である。また数量化の結果は選ばれた調査対象に依存するので，予測や分類を考えるときは，偏りのない対象を選ばなければならない。近年では，K-L型数量化，最小次元解析などの数量化の方法が開発される一方，コンピューターによる図的表示を工夫して分析結果を解釈しやすくする試みもなされている。

　数量化に似た考え方は欧米にもみられる。1940年代から50年代にかけてガットマンL.Guttmanは比較判断による数量化や第Ⅲ類に似た尺度解析法を考案した。また70年前後からフランスのバンゼクリJ.P.Benzécriは第Ⅲ類にきわめて似た手法（correspondence analysis）を開発した。日仏間の研究交流も行われている。
執筆者：岩坪 秀一

出典　株式会社平凡社「改訂新版　世界大百科事典」