生産関数（読み）せいさんかんすう（英語表記）production function 英語

精選版 日本国語大辞典

せいさん‐かんすう‥クヮンスウ【生産関数】

1. 〘 名詞 〙 一定の単位期間について、生産要素の投入量と生産物の産出量の技術的関係を表わす関数。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

生産関数
せいさんかんすう
production function 英語
fonction de production フランス語
Produktions funktion ドイツ語

生産要素の投入量と、それにより達成可能な最大産出量との間に定まる技術的関係を示すもの。生産物Yの生産には、労働Lや資本Kなどの生産要素を必要とする。このとき生産関数は、
　　Y=f(K,L)
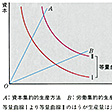
と表される。生産関数の満たすべき基本的仮定は、(1)資本と労働とのそれぞれの限界生産力は正であり、(2)資本と労働との技術的限界代替率は逓減(ていげん)する、の二つである。基本的仮定(1)は、資本（労働）投入が不変のとき、労働（資本）を増やすとそれだけ生産量も増加する、という常識的なものである。基本的仮定(2)の資本と労働との技術的限界代替率とは、生産量を一定量Y₀に保つときに、労働を追加的に1単位増加（減少）させると資本が何単位減少（増加）するかを測るものである。ある一定の生産量を生産する場合、労働が増えるにつれて技術的限界代替率はしだいに減少する、というのが基本的仮定(2)の内容である。これは、労働が増加すると、相対的に資本が希少となり、資本1単位の減少を埋め合わせるのに必要な労働の増加分が大きくなることを意味する。また、この基本的仮定(2)は、等（生産）量曲線（ある一定の生産量を生産するのに必要な労働と資本との組合せを示す曲線）が原点に対して凸であることを示している。

　一定量を生産する場合、相対的に資本を多く投入する方法（資本集約的生産方法）や、反対に相対的に労働を多く投入する方法（労働集約的生産方法）がある。このように一方の生産要素を他の生産要素に代替して投入できる場合、その生産要素間の代替の程度の測度を代替の弾力性とよび、労働・資本間の代替の弾力性は、労働の資本集約度の変化率を技術的限界代替率の変化率で割った比率と定義される。その値がゼロであると資本と労働の代替可能性はまったくなく、それらはつねに一定比率で投入される。その値が大きければ大きいほど、資本と労働との代替可能性は大きいのである。

　資本と労働との投入を同時に2倍（m倍）にすると、生産量もまた2倍（m倍）になるとき、この生産関数は一次同次である、あるいは規模に関して収穫不変である、という。

［内島敏之］

生産関数の型

生産関数の具体的な形状については種々の考え方があるが、もっとも代表的な具体例としては、コブ‐ダグラス生産関数とCES生産関数とがあげられる。

　コブ‐ダグラス生産関数はC・W・コブとP・H・ダグラスとによって提案されたもので、
　　Y=aK^αL^β
で示される。a、α、βは正の定数であり、α+β=1であると、生産関数は一次同次であり、α（β）が1より小さいと、資本（労働）の限界生産力は逓減的である。α（β）は資本（労働）分配率、つまり所得に占める利潤（賃金総額）の割合を示している。

　CES（constant elasticity of substitution）生産関数は、代替の弾力性が一定である生産関数で、K・J・アロー、H・B・チェネリ、B・S・ミンハス、R・M・ソローの4人によって提案されたものである。彼らは現実のデータから労働生産性（労働の平均生産力）は賃金率と高い相関関係をもつことを知り、この関係からCES生産関数を導出した。この生産関数は、
　　Y=a［αK^-ρ+βL^-ρ］^-1/ρ
と表される。a、α、βは正の定数であり、α+β=1のときには一次同次である。ρは代替パラメーターであり、代替の弾力性は1+ρの逆数に等しい。ρがゼロのときには代替の弾力性は1となり、生産関数はコブ‐ダグラス型となる。また、ρが無限大のときには代替の弾力性はゼロであり、生産量の対要素投入量比率を示す生産係数は固定的となる。このような生産関数はレオンチェフ‐ハロッド型とよばれる。

［内島敏之］

『荒憲治郎著『経済成長論』（1969・岩波書店）』▽『佐藤和夫著『生産関数の理論』（1975・創文社）』

[参照項目] | アロー | 限界生産力 | コブ‐ダグラス生産関数 | 代替の弾力性 | レオンチェフ

生産関数

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

生産関数 (せいさんかんすう)
production function

一企業または経済全体でどれだけの資源・原材料を投入すれば，どれだけの生産を行えるかを表した数学的関係式。一般に，この関係はその企業または経済のもっている技術的知識によって決まるから，生産関数とは当該経済主体のもっている生産技術に関する知識全体の抽象的表現である。したがって，生産関数は技術の変化（技術進歩）に伴って変化すると考えられる。たとえば農業で，米穀の生産トン数Rは，米穀生産に使用される労働者数L，肥料投入量S，土地面積T，等の投入量が変化すれば変わってくる。さまざまな投入の組合せ（L，S，T，……）のもとでの最大可能生産量Rは，R＝F（L，S，T，……）のように表すことができる。この関数Fが生産関数である。

　生産関数の具体的な形状については種々の考え方がある。最も代表的な生産関数はC.W.コブとP.H.ダグラスが考案したコブ=ダグラス生産関数で，y＝Ax_i^αx_j^βの形で表される。x_i，x_jはおのおの投入量，yは産出量を表し，α＋β＝1なる仮定すなわち代替弾力性が1に等しいという仮定が設けられている。

　コブ=ダグラス生産関数をより一般化したのがCES（constant elasticity of substitution）生産関数で，K.J.アロー，H.B.チェネリー，B.S.ミンハス，R.M.ソローの4人によって発表された。これは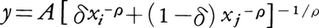の形で表され，このとき代替弾力性は1/（1＋ρ）なる一定値となる。したがってρ＝0のとき代替の弾力性は1に等しくなり，この意味でCES生産関数はその特殊型としてコブ=ダグラス生産関数を含むのである。
執筆者：奥野 正寛

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

生産関数
せいさんかんすう
production function

単位期間における生産要素の投入量と生産物の産出量との間にある一定の技術的関係を表す関数。産出量Xと生産要素の投入量 (y₁ ，y₂ ，…，y_n) の間の技術的関係は，x＝f(y₁，y₂，…，y_n) という関係で表わされ，この関数fを生産関数という。ただし，複数の投入物，産出物 (X₁ ，X₂ ，…，X_n) の間の技術的関係は，g(X₁，X₂，…，X_n)＝0 という陰関数の形でも表現されうる。生産関数は最も経済効率の高い生産要素の組合せを選択するための手掛りとなる。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

生産関数【せいさんかんすう】

生産要素（労働，土地，資本など）の組合せからどれだけの産出量が得られるかを表す関係式で，その経済主体がその生産に関してどれほどの技術・知識を有しているかを抽象的に表現する方法。技術的に代替できる生産要素の組合せのなかで，最も有利な組合せを決めるための手がかりとなる。生産要素の投入量をすべて２倍にしたときに産出量が２倍以上になれば，生産技術（生産関数）が〈規模に関して収穫逓増〉のもとにあるといい，ちょうど２倍ならば〈規模に関して収穫一定〉，２倍以下ならば〈規模に関して収穫逓減〉という。
→関連項目ソロー

出典　株式会社平凡社

世界大百科事典（旧版）内の生産関数の言及

【アクティビティ･アナリシス】より

…〈活動分析〉と訳される。生産活動を分析する場合，経済学では伝統的に生産関数が鍵概念として利用されてきた。生産関数は，生産物の産出量と資本･労働･原材料などの生産要素の投入量とを数量的に関連づける関係であるが，この関係を背後から規定するのは生産技術であるとされる。…

【生産要素】より

…企業家は，一定の生産技術のもとでこの生産要素を利用･変形して生産物を産出する。この関係を数学的に表現したものが生産関数である。【牧野 文夫】。…

【ミクロ経済学】より

…企業が販売量を変更することにより価格を変化させることができる場合は不完全競争であり，企業にとって市場価格が変更不能の場合は完全競争である。生産要素の生産への投入量と生産物の産出量の間の技術的関係(生産関数)の許す範囲で，生産物の販売収入と生産要素購入費用の差である利潤を最大にするように，企業は生産物の供給と生産要素の需要を決定する。諸価格が変化すれば，完全競争の場合の需要量，供給量は変化する。…

※「生産関数」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」