オストワルト表色系（読み）おすとわるとひょうしょくけい（英語表記）Ostwald system

日本大百科全書(ニッポニカ)

オストワルト表色系
おすとわるとひょうしょくけい
Ostwald system

ドイツの化学者F・W・オストワルトが考案した、関連色を表示するためのシステム。オストワルト記号を用いて関連色を表示する。ここで関連色とは、ほかの色と相互に関連して見えている面に属するように知覚される色である。たとえば、物体表面の色を、通常の背景、または周辺にある他の物体表面の色とともに見るような場合の色が関連色である。

　オストワルトは色を関連色と無関連色に区別した。無関連色は、他の色から独立している面に属するように知覚される色である。たとえば、分光器の視野のように、暗黒の周辺視野で光の色を見るような場合の色や、闇夜に単独で点灯する信号灯のように、他に比較するものがない色が無関連色である。オストワルトは「無関連色は白色と純色のみを含むが、関連色はこれらの他に黒が加わって構成される」とした。

　オストワルトは理想的な白W、理想的な黒B、完全色Cを基本的な要素として、同一色相のすべての関連色（以下で、単に色とよぶ）はこれら三つの要素の含有量によって表されるとした。ここで、Wはすべての波長の光を完全に反射する理想的な白（視感反射率Y＝100％）、Bはすべての波長の光を完全に吸収する理想的な黒（Y＝0％）を表す。W、B、Cの含有量をそれぞれ白色量、黒色量、純色量とよび、量記号W、B、Cで表す。W、B、Cの間にはW＋B＋C＝1の関係がある。視感反射率0％の理想的な黒Bは眼(め)に見えないため、この式は、すべての色がW量の理想的な白とC量の完全色の加法混色で得られることを示す。また、オストワルトは完全色（C＝1）を図Aに示す(a)～(d)の四つのタイプの純色に分類した。

　タイプ(a)は補色波長対をなす二つの波長λ₁とλ₂（加法混色で特定の無彩色をつくることができる二つの単色光の波長）の間の波長領域で光を完全に反射し、それ以外の領域では光を完全に吸収するような分光反射率をもつ純色。タイプ(b)は波長λ₁とλ₂の間の波長領域で光を完全に吸収し、それ以外の領域では光を完全に反射するような分光反射率をもつ純色。タイプ(b)はタイプ(a)の補色である。タイプ(c)は補色波長をもたない波長λ₃（補色波長対が定義できない波長）より長波長側で光を完全に反射し、それ以外の領域では光を完全に吸収するような分光反射率をもつ純色。タイプ(d)は波長λ₃より長波長側で光を完全に吸収し、それ以外の領域では光を完全に反射するような分光反射率をもつ純色。タイプ(d)はタイプ(c)の補色である。

［佐藤雅子］

ヘリングの反対色説

黄みの赤、青みの赤というように、経験的に、赤と黄、赤と青の色感覚は共存できる。しかし、緑みを帯びた赤や、赤みを帯びた緑は知覚できないので、赤と緑の色感覚は共存できない。

　生理学者にして心理学者でもあるE・ヘリングは「視覚系には赤の反応と緑の反応を拮抗(きっこう)させる組織が存在し、これらの反応の相互の打ち消し合いの結果、残った反応が色の知覚をもたらす。そのため、赤か緑のいずれかの色感覚しか生じない（完全に打ち消し合ったときは色みをまったく感じない）」と考え、赤と緑を反対色とよんだ。また、同様の視覚現象を根拠として、黄と青や、白と黒も反対色とよんだ。ヘリングの反対色説は「視覚系には赤―緑、黄―青、白―黒の各反対色に応答する三つの機構が存在し、すべての色の特性はこれらの機構の応答量の割合で表される」とするものである。

［佐藤雅子］

色相環

太陽光のスペクトルに現れる赤、オレンジ、黄、…、菫(すみれ)（分光分布に長波長成分を含まないので、赤みがまったくない）の次に紫系（短波長成分のほかに長波長成分も含むので、多かれ少なかれ赤みを帯びる）を加え、その次に赤が並ぶように色相を円周上に配置したものを色相環とよぶ。オストワルトの色相環はヘリングの2対の反対色を基本4色相の黄（Yellow）、赤（Red）、青（Ultramarine Blue）、緑（Sea Green）とする。それらの色相の中間にオレンジ（Orange）、紫（Purple）、青緑（Turquoise）、黄緑（Leaf Green）を加えて8色相とし、さらに、これらの各色相を三分割して得られる計24色相で色相環を構成する（図B参照）。オストワルトの色相は図Bに示すように、Yellowの1からLeaf Greenの24に至る一連の数字記号（色相番号）を用いて表す。

　これら24の色相は、Nが色相を表すとすると、完全色（N）と（N＋2）の加法混色によって生じる色は完全色（N＋1）と同じ主波長（特定の無彩色刺激と適当な比率で加法混色することによって、試料色刺激と等しい色をつくることのできる単色光の波長）または補色主波長（紫系の試料の場合、試料色刺激と適当な比率で加法混色することによって、特定の無彩色刺激と同じ色をつくることのできる単色光の波長。ここで色刺激とは眼に入射して色感覚をもたらす可視放射のことである）をもつという原理によって定められている。この原理を拡張すると、色相（N＋12）と（N）の二つの色は補色の関係になり、色相環上で相対する色相の色は互いに補色である。

　なお、色相の表示には、1から24に至る一連の数字記号（色相番号）のほかに、図Bに示すように、数字記号と文字記号を組み合わせた1Y、2Y、3Y、1O、2O、3Oなども用いられる。たとえば、数字記号1と1Y、数字記号7と1Rは、それぞれ同じ色相を表す。

［佐藤雅子］

グレースケール

白および黒を両端におき、その間に、明るさの間隔が等しくなるように選択した無彩色を配列して得られる明るさのスケールをグレースケールとよぶ。グレースケールは、明るさが均等な間隔で段階をなしていることが必要とされ、マンセルのバリュースケールはその代表の一つである。オストワルトのグレースケールは、「感覚量は刺激（物理量）の対数に比例する」とするフェヒナー則に基づいて構成されている。このようなスケールでは黒の近くで段階の差が視覚的に圧縮されるが、オストワルトは近似的に視覚的均等性が成り立つと仮定して、フェヒナー則によってグレースケールを構成した。

　理論的には、理想的な白（W＝1）および黒（B＝1）を両端に配置し、各段階の無彩色の視感反射率をフェヒナー則に基づき、対数尺度で等間隔に（等比級数をなすように）定めた。しかし、理想的な白および黒は実現が不可能なことから、実際には、もっとも明るい白色の対数値を2.00（視感反射率Y＝100％：白色量W＝1）に替えて1.95（Y＝89.0％：W＝0.890）とし、また、もっとも暗い黒の対数値を0.55（Y＝3.5％：W＝0.035）として、15段階のグレースケールを作成した。

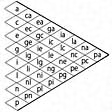
　オストワルトは、グレースケールを構成する各段階の無彩色をaからp（ただし、jは間違いを避けるために除く）に至る文字記号を用いて表した。1.95のもっとも明るい白色は文字記号aによって、以下、0.10ピッチで暗くなり0.55に至る各段階の無彩色は明るさの順に文字記号b、c、d、…、pによって表示した。その後、オストワルトは、より実用的なスケールとして、a、c、e、g、i、l、n、pのように1段抜きに8段階に簡略化したグレースケールを推奨した。

　無彩色は完全色をまったく含まないので、白色量および黒色量のみで表される（W＋B＝1）。この八つのローマ字記号a、c、e、g、i、l、n、pが表示する無彩色の白色量W、および黒色量Bを表に示す。この表は、以下のように用いることを考慮して、無彩色の表示記号を第3欄に、各無彩色を表す白色量W、黒色量Bを、それぞれ第1欄、第2欄に記載してある。

　有彩色は色相の表示記号のほかに白色量Wおよび黒色量Bを用いて表示する（後記）。これらの量の表示は数値ではなく記号を用いて行う。そのために、白色量Wおよび黒色量Bの特定の値に対応する記号が、この表に基づいて定められている。白色量の表示では、この表の最初の欄の白色量Wのそれぞれに最後の欄のローマ字記号a、c、e、g、i、l、n、pを対応させ、黒色量の表示では、次の欄の黒色量Bのそれぞれに同じローマ字記号a、c、e、g、i、l、n、pを対応させる。たとえば、白色量を表す文字記号が「e」の場合はW＝0.350を表し、黒色量を表す文字記号が同じく「e」の場合はB＝0.650を表す。

［佐藤雅子］

同色相三角形と色立体

オストワルトは、グレースケールで無彩軸（明るさを表す垂直軸）を構成し、この軸の周りに色相環を配置して、無彩系列（後記）と純色系列とを関係づけた。

　オストワルトは、理想的な白Wが上、理想的な黒Bが下になるようにグレースケールを垂直に立てて、その中央の無彩色（中明度のグレー）を中心とし、無彩軸の長さの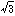/2倍を半径とする、無彩軸に直交する平面における円周上に完全色Cによる色相環を配置した。これにより色相環上の1点（一つの色相をもつ完全色C）と無彩軸を含む平面上で、正三角形WBCが得られる（図C参照）。オストワルトは理想的な白色刺激と任意に与えられた一つの完全色の色刺激との加法混色で得られる色（すべて同一の主波長または補色主波長をもつ）はすべて同一色相の色（厳密には、一般に、色相が多少変化する）とみなし、図Cに示すように、それらの色を正三角形WBC上で表した（理想的な黒は眼に見えないため、この三角形上の色はいずれも理想的な白と完全色との加法混色で得られる）。この三角形をオストワルトの同色相三角形とよぶ。図CにおいてC、W、Bを表す数値はW＋B＋C＝100とする場合のものである。

　同色相三角形の一辺WB上では純色量C＝0であり、この辺に沿って、理想的な白から黒に至る無彩色がフェヒナー則に従って明るさの順に配列している。これらの無彩色の系列を無彩系列とよぶ。純色量C＝1（図Cでは100）の完全色は三角形の頂点Cに位置する。完全色と同じ色相をもつ有彩色の白色量Wおよび黒色量Bはそれぞれ、三角形の辺WC、辺BCに沿う尺度に基づいて表される。これらの尺度もまた、フェヒナー則に従い、対数に関して等間隔に目盛られている（図C参照）。

　三角形の辺WCに沿う有彩色は理想的な白と完全色のみを含み（W＋C＝1）、黒色量B＝0である。これらの色の系列を明澄系列とよぶ。また、辺BCに沿う有彩色は白色量W＝0であり、理想的な白をまったく含まない（B＋C＝1）。これらの色の系列を暗澄系列とよぶ。この二つの系列は仮想のものであり、実在する色材によって実現することはできない。

　三角形の辺WCに平行な一つの直線上に位置する有彩色は黒色量Bが相等しい。これらの色の系列を等黒系列（アイソ・トーン系列）とよぶ。また、辺BCに平行な一つの直線上に位置する有彩色は白色量Wが相等しい。これらの色の系列を等白系列（アイソ・ティント系列）とよぶ。

　三角形の辺WBに平行（無彩軸に平行）な一つの直線上に位置する有彩色は、いずれも純色量と白色量との比C／W（オストワルト純度とよぶ）が相等しい。これらの色の系列を等純系列（アイソ・クローム系列）とよぶ。同じ等純系列に属する有彩色は、視感反射率のみが異なり、いずれも同一の色度座標（XYZ表色系の二次元座標）をもつ。

　また、白色量W、黒色量B、純色量Cが同一で、色相のみが異なる有彩色をアイソ・バレント・カラーといい、これらの色の系列をアイソ・バレント系列とよぶ。

　完全色Cと理想的な白Wおよび黒Bは仮想の色であり、実際にはつくることができない。同様に、明澄系列と暗澄系列も実現はできない。図Cにおいて太線で画された三角形の部分は、オストワルト色票集の色票によって実現できる同色相三角形の範囲を示す。無彩軸を共通の軸として、この太線で画された実現可能な等色相三角形を、色相環の順に従って等間隔に配置すると、図Dに示すような複円錐状の立体が得られる。この立体をオストワルトの色立体とよぶ。図中央部に現れている二つの断面は、色相の異なる二つの等色相三角形を示す。

［佐藤雅子］

オストワルト色票の表示記号（オストワルト記号）

白色量Wおよび黒色量Bが与えられると、W＋B＋C＝1の関係から純色量Cは既知となる。そこで、実現可能な等色相三角形（図Cにおいて太線で画された三角形）内に含まれる有彩色は、色相記号の次に白色量Wに対応する文字記号（等白系列の種類を表す）を、さらにその後に、黒色量Bに対応する文字記号（等黒系列の種類を表す）を並べて表示する。一方、無彩色は色相をもたないので、白色量Wおよび黒色量Bに対応する文字記号のみで表示する。

　白色量Wおよび黒色量Bと文字記号との対応は、前記の表および本文説明のとおりである。これらの対応を図Cにおいて太線で画された三角形の部分に適用すると図Eが得られる。たとえば、7 pg（または1R pg）は色相番号7、W＝0.035、B＝0.780、C＝1－（W＋B）＝0.185の有彩色を表す（表および図C参照）。この色は通常、ワインとよばれている。無彩色は前記の表から明らかなように、原則として、aa、cc、eeなどのように表示するが、一般にはa、c、eなどのように略記する。

［佐藤雅子］

[参照項目] | 色 | オストワルト | 補色

完全色の分光反射率〔図A〕

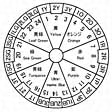
オストワルト色相環〔図B〕

白色量および黒色量の表示記号〔表〕

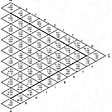
オストワルト同色相三角形〔図C〕

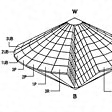
オストワルト色立体と等色相断面〔図D〕

文字記号による白色量および黒色量の表示…

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

オストワルト表色系【オストワルトひょうしょくけい】

F.W.オストワルトが考案した表色系。すべての物体色は各色相に属する純色と白色と黒色が適当に混合してできると考え，色相の番号（１〜24），白色量，黒色量（それぞれ文字で示す）の三つで表示する。調和する色が見つけやすく，美術界で用いられる。
→関連項目色

出典　株式会社平凡社