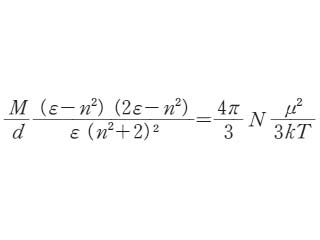オンサガーの式（読み）オンサガーノシキ

化学辞典 第2版

オンサガーの式
オンサガーノシキ
Onsager equation

【Ⅰ】強電解質溶液の当量電気伝導率の濃度変化を表す式．1927年L. Onsager(オンサガー)がイオン分布に関するデバイ-ヒュッケルの理論を拡張して提出した．z_＋-z_－型強電解質溶液の当量電気伝導率Λは，次式で表される．

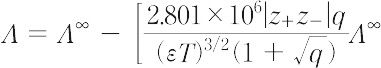
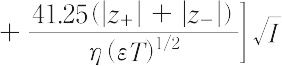
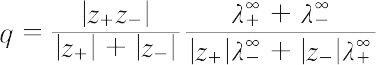
ここで，εは溶媒の誘電率，ηは粘度，Tは絶対温度，Iは溶液のイオン強度，Λ^∞ は無限希釈溶液の当量電気伝導率，λ_＋^∞ および λ_－^∞ はそれぞれ無限希釈溶液におけるカチオンおよびアニオンの当量イオン伝導率である．上式の[　]内の第一項は非対称効果あるいは緩和効果，第二項は電気泳動効果による減少分を表す．また，上式は次のような形に書くことができる．

Λ ＝ Λ^∞ － (B₁Λ^∞ ＋ B₂)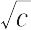

ただし，B₁，B₂ は定数，cは濃度である．これはコールラウシュの法則(平方根則)と一致する．上記のオサンガーの式は，その誘導過程に含まれる近似のために十分希薄な溶液についてしか成立しない．【Ⅱ】極性液体の誘電率と個々の分子の双極子モーメントとの関係を表す式として，1936年Onsagerにより提出された式．液体内における内部電場として，空洞電場と反作用電場とを考慮すると，誘電率εと双極子モーメントμとの関係は，次式で表される．

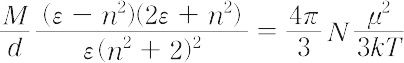
ここで，Mは分子量，dは密度，nは屈折率，Nはアボガドロ定数，kはボルツマン定数，Tは絶対温度である．この式は，粗い近似のもとに導出されているが，多くの液体に対してよく成立することが知られている．

出典　森北出版「化学辞典（第2版）」

法則の辞典

オンサガーの式【Onsager's equation of dielectric constant】

極性液体の誘電率（ε）と，分子の双極子モーメント（μ）との関係を表す理論式．M を分子量，d を密度，n を屈折率，N をアヴォガドロ定数＊，k をボルツマン定数＊，T を絶対温度とすると，下のような式で表される．

多くの液体に対してよく成立する関係式である．

オンサガーの式【Onsager's equation】

「オンサガーの伝導度の公式」のページをご覧ください。

出典　朝倉書店