改訂新版 世界大百科事典 「リーマン面」の意味・わかりやすい解説
リーマン面 (リーマンめん)
Riemann surface
複素一次元解析多様体のことである。すなわち,連結なハウスドルフ空間Sにおいて,開集合Uの族による被覆と,各Uから複素平面の開集合の上への位相写像φu(これを局所座標という)で,U∩V≠φのときφu◦φv⁻1が正則関数となっているものをいっしょに考えたものである。
Sの上の複素数値関数fは,各局所座標に対してf◦φu⁻1が,通常の意味の正則関数となっているとき,Sで正則であるという。1851年,G.リーマンは学位論文において,多項式Fの定める代数方程式F(z,w)=0を解いて得られる多価関数w=w(z)(代数関数という)を研究するに際し,複素平面上に何葉かの重なりあった面を考えて,その上でw(z)が1価となるようにした。
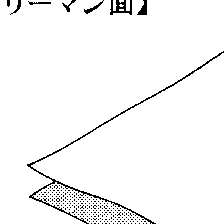
図はw2-z=0に対応するリーマン面の一部である。中央の点は原点z=0で,このシートのつながり方は次のようになっている。すなわち,上のシートで原点を正の向きにまわると,継目から下のシートに入り,そこで原点をさらにまわると継目から再び上のシートに出てくる。
リーマンは,このような面の位相的性質と代数関数の性質との関係を研究した。K.ワイヤーシュトラスは,解析接続による解析関数を導入して,多価関数を扱う方法を与え,リーマンと同じころ,代数関数を研究した。この解析関数も,複素平面をおおう一つの面と考えることができる。
このように,平面以外のところで正則関数を考えるための土台がリーマン面なのである。これらを抽象して,初めに述べた定義を与えたのは,C.ワイルである。現在では,この定義がふつう用いられ,リーマン面は複素一次元解析多様体の別称にすぎなくなった。コンパクトなリーマン面は,閉リーマン面と呼ばれる。リーマン自身が扱ったのは,これであって,研究には関数論的・代数的・代数幾何的方法などがある。コンパクトでないリーマン面は開リーマン面といい,現代の関数論の研究対象の一つになっている。
執筆者:及川 廣太郎
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報