多価関数（読み）タカカンスウ

デジタル大辞泉

たか‐かんすう〔‐クワンスウ〕【多価関数】

独立変数の一つの値に対して従属変数の値が二つ以上対応しうるような関数。

出典　小学館

精選版 日本国語大辞典

たか‐かんすう‥クヮンスウ【多価関数】

1. 〘 名詞 〙 独立変数ｘの一つの値に対して、従属変数ｙの値が二つ以上定まるような関数。ｘの一つの値に対してｙの値が二つ定まるものを二価関数、三つ定まるものを三価関数、一般にｎ個定まるものをｎ価関数といい、無限個定まるものを無限多価関数という。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

多価関数
たかかんすう

通常、関数というときには、変数xの値が決まれば、それに伴って変数yの値がただ一つ決まる場合をいう。しかし、ときには、xの値に同時にいくつものyの値が対応してくることもある。たとえば、xに対して、二乗すればxになる数（すなわちxの平方根）を対応させる場合には、x＞0ならばつねに二つのyの値を得る。このような関数を多価関数という。これは、前述の例のように、逆関数の考察において生ずる場合が多い。

　f(x)が複素変数xの解析関数である場合には、多価関数についての興味深い理論ができあがる。たとえば、上記の関数　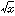　は、x=1で1という値をとり連続であるとすれば、|x-1|＜1では、普通の、値が一つに定まる関数として確定する。この関数は、この範囲ではxの正則関数（領域内の各点で微分可能な複素関数）であるが、これを解析接続していくと、x=0を除いては複素平面全体に接続可能である。そして、x=0を1回回ってx=1に戻れば、その値は-1になる。したがって、x=0の周りを回れないようにすれば、たとえば、負の実軸上で関数を定義しないことにすれば、一価関数として値が確定することになる。

　リーマンは、さらに、より自然な形で、一価関数としての考察をすることを考えた。いま、二枚の複素平面を用意し、それを重ねて、ともに負の実軸に沿って切り、上の平面の上側の縁と下の平面の下側の縁、上の平面の下側の縁と下の平面の上側の縁をはり合わせてできる面を考えると、この上では　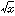　は一価としてとらえられる。このように構成された面をリーマン面という。リーマン面は、ワイルによって精密な理論に仕上げられ（1913）、今日の複素解析多様体の理論へと発展している。

［竹之内脩］

[参照項目] | 解析関数 | 関数

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

多価関数
たかかんすう
many-valued function

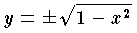関数 y＝f(x) において，1つの x に対し，y の価がたかだか n 個定まるとき，この関数は，x の n 価関数であるといい，2価以上の関数を総称して多価関数という。たとえば関数 は2価関数，また逆正弦関数 y＝ sin ^-1x は無限価の多価関数である。現在では，関数というのを1価に限定する (→一価関数 ) が，逆関数を考えたりするときに出てくる。それを1価にするために，定義域を限定したり，リーマン面を考えたりする。

出典　ブリタニカ国際大百科事典 小項目事典