精選版 日本国語大辞典 「指数法則」の意味・読み・例文・類語
しすう‐ほうそく‥ハフソク【指数法則】
改訂新版 世界大百科事典 「指数法則」の意味・わかりやすい解説
指数法則 (しすうほうそく)
exponential law
a,bを任意の数(実数または複素数)とし,m,nを正の整数とすると,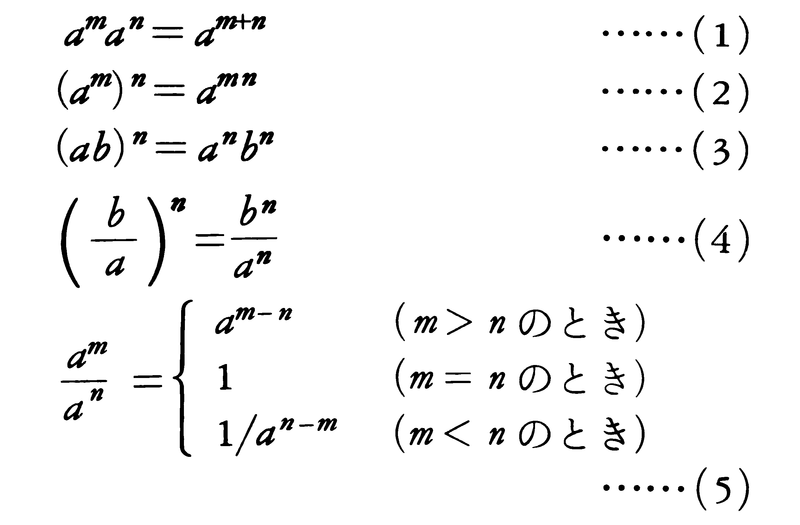
ただし,(4),(5)においてはa≠0とする。
上の(1)~(5)を(指数が正の整数の場合の)指数法則という。
正の数aに対してaxの定義を,指数xが任意の実数の場合まで拡張する。そのとき,拡張した範囲でも指数法則が成り立つように定義しなければならない。
任意のa>0と正の整数nに対してbn=aとなる正の数bはただ一つ定まる。このbをaの正のn乗根といい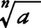 と書く。すなわち,
と書く。すなわち,
今後a,bは正の数を表すことにして,いちいちそのことを断らない。
まず(5)が整数m,nの符号や大小に関係なくam/an=am⁻nと書けるためには,a0=an⁻n=an/an=1,したがってa⁻n=a0⁻n=a0/an=1/anとなるべきである。よって,
a0=1,a⁻n=1/an (n>0) ……(7)
と定義する。次に,正の有理数rはr=m/n(m,nは正の整数)と表されるから,指数が有理数の場合にも,(2)が成り立つためには(ar)n=arn=amとなるべきである。だから(6)により,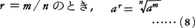
と定義すればよい。
とくにm=1のときは,

と定義したことになる。指数が負の有理数の場合については,負の整数の場合(7)と同様に考えて,
a⁻r=1/ar (rは正の有理数) ……(7′)
と定義する。以上の定義により,(4),(5)はそれぞれ(3),(1)で表されるから,指数法則は次の三つの式にまとめられる。
aras=ar⁺s ……(1′)
(ar)s=ars ……(2′)
(ab)r=arbr (r,sは有理数) ……(3′)
次に,任意の実数xに対して,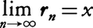 なる有理数列{rn}をとると,数列
なる有理数列{rn}をとると,数列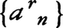 は収束して,その極限値は,xに収束する有理数列{rn}のとり方に関係なく,xによって定まる。そこで,
は収束して,その極限値は,xに収束する有理数列{rn}のとり方に関係なく,xによって定まる。そこで,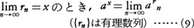
と定義すると,すべての実数xに対してaxが定義されて,指数法則が成り立つ。すなわち,a>0,b>0のとき,任意の実数x,yに対して次の各等式が成立する。
axay=ax⁺y ……(1″)
(ax)y=axy ……(2″)
(ab)x=axbx ……(3″)
執筆者:伊藤 清三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報
ブリタニカ国際大百科事典 小項目事典 「指数法則」の意味・わかりやすい解説
指数法則
しすうほうそく
law of exponent
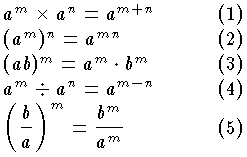
出典 ブリタニカ国際大百科事典 小項目事典ブリタニカ国際大百科事典 小項目事典について 情報
法則の辞典 「指数法則」の解説
指数法則【law of exponents】
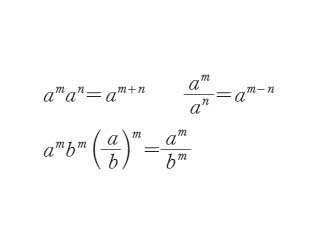
この関係は,m,n が整数のとき,または a,b が正で m,n が実数の場合において成立する
世界大百科事典(旧版)内の指数法則の言及
【べき(冪∥羃)】より
…なお,2乗のことを自乗,または平方,3乗のことを立方ともいう。
[指数法則]
数,変数,式,または関数x,yと自然数m,nについて,次が成り立つ。 xm×xn=xm+n (xm)n=xmn (x×y)n=xn×yn (x÷y)n=xn÷ynここで,自然数nについて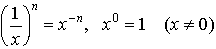 で表すと,べき指数,指数法則は整数まで拡張される。…
で表すと,べき指数,指数法則は整数まで拡張される。…
※「指数法則」について言及している用語解説の一部を掲載しています。
出典|株式会社平凡社「世界大百科事典(旧版)」
関連語をあわせて調べる
春になって暖かくなりかけた頃、急に寒さが戻って、地面などがまた凍りつく。《 季語・春 》[初出の実例]「七瀬御秡 同晦日也。〈略〉雪汁いてかへる」(出典:俳諧・誹諧初学抄(1641)初春)...

