記数法（読み）キスウホウ（英語表記）numeration system

デジタル大辞泉

きすう‐ほう〔‐ハフ〕【記数法】

数字を使って数を表す方法。一般には、アラビア数字を使った十進法による位取り記数法が用いられる。

出典　小学館

精選版 日本国語大辞典

きすう‐ほう‥ハフ【記数法】

1. 〘 名詞 〙 数を数字で表わす方法。古くは個々の数に一つずつ数字をあてていたが、今日では、いわゆる位取りの考えを用い、ごく限られた個数の数字ですべての数を表わす方法がとられる。十進法、二進法など。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕
   1. [初出の実例]「インド式の記数法に於ては、例へば二万七千五百二十九は之を27529と書く」(出典：零の発見（1939）〈吉田洋一〉六)

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

記数法 (きすうほう)
numeration system

言葉を文字で記すように，数を記号，文字などで表すしかた。日常われわれはアラビア数字0，1，2，……，9，または漢数字一，二，三，……，十，百，千，万，億，兆を使って数を表示している。例えば，352701815は三億五千二百七十万千八百十五である。前者の表し方には次の三つの特徴がある。（1）十進法，（2）桁を数の位置で表す，すなわち位取りの原則，（3）10個の数字だけを使っている。文化圏によって種々の記数法が考案され，使われてきたが，この3特徴すべて備えたものは6世紀までにインドで確立されたものと考えられている。

　人類がどのように数を認識し，表示してきたかを知るのはたいへんむずかしい問題である。もともとは，個数の認識から始まり，それが自然数へと発展した。個数または自然数を表すのに，地面に線を描く，木にきずをつける，石を並べる，棒を並べる，あるいは縄の結び目などを利用した。やがて，石を並べるにしても，それのいくつかをひとまとめにして単位を作って表すほうがわかりやすいことに気づいた。各単位がいくつからなるかは，部族，文化圏で違っていたが，2，3，5，10，12，20，60などが使われた。ここに，二進法，……，十進法，……，六十進法などの萌芽が見られる。しかし，これが今日われわれがいう意味での何進法かになるのにはもう一つ飛躍が必要である。これを十進法で見てみよう。われわれが日常に使っている数の表し方で，例えば8962は8000＋900＋60＋2を意味する。これは10を単位としているが，それだけでなく，1の桁，10の桁，100の桁，1000の桁というように，1単位10の10倍を新しい単位とし，その10倍もまた単位とする……と続けていく。10を基本単位として数を表すので，十進法といわれる。もともとは，人間の手の指の数が10本であることから，10ごとにまとめて物を数えるようになり，そこから十進法が発達してきたことはまちがいない。上記十進法の10のかわりに2を使ったものを二進法という。例えば，十進法での11は二進法では1011となる。二進法は近年コンピューターで使われている。これは，電流が流れる，流れないを1，0に対応させて計算したり，論理回路を作ったりしている。われわれがコンピューターを使うときはたいてい十進法を使うが，コンピューターの内部で二進法になおして計算し，結果をまた十進法になおす。一般に，一つの自然数nを単位として，十進法，二進法と同様に，一般の自然数を表すしかたをn進法という。0からn－1までを表す記号を用意すれば，1，n，n²，n³，……をそれぞれ1桁目，2桁目，3桁目の単位として，すべての自然数が表記できる。自然数を表記するためには何進法でもさしつかえないが，十進法がもっとも日常的である。

　そのほか，長さ，面積，体積，重さ，時間などに十二進法（1フート＝12インチ），十六進法（1ポンド＝16オンス，1オンス＝16ドラム），六十進法（1時間＝60分，1分＝60秒）などが使われるが，それらは統一的，組織的なものではない（例えば，60時間を表す単位はない）。歴史的にみると，十進法以外に，六十進法がメソポタミアで組織的に使われた。

　位取りの原則を利用した記数法は4000年ほど昔からメソポタミアで発達した。この場合，ある桁に数字がないことを意味する記号，すなわちゼロが必要になる。メソポタミアでは前4世紀までにゼロを表す記号として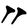が使われるようになった。しかし，これは完全なものではなかった。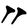は数字の間にしか使われなかったので，例えば，は11×（60）³＋3×（60）²，11×（60）²＋3×60，11×60＋3のいずれをも表した。しかし，たいていは前後関係でどれかがわかり，実用上はあまり不便でなかったのであろう。注目すべきことは，が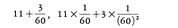，の意味にも使われたことである。漢字による表示は十進法であるが，1から9までを表す漢字と，桁を表す特別な字が用意されていて，その組合せで数を記す。この方法では日常生活には困らないが，いくらでも大きい数字を表すことはできない。エジプトでも十進法であったが，漢字より少し原始的で，各桁ごとの単位

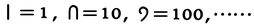を用意して，それを重ね合わせることで数字を表した。ギリシアのアッティカ式，ローマ数字もこれに近い。ギリシアのイオニア式は各数ごとの記号は少なくてすむという点では優れているが，各桁ごとで記号を変えているので，たくさんの記号を用意しなければならず繁雑である。中国では算木による記数法も用いられた。これはインドの方法に近いが，0が使われるようになったのはずっと後で，それまでは0の代りに空欄が利用された。赤の算木を使って正の数を，黒の算木で負の数を表したことは注目すべきことである。

　各記数法にそれぞれの長所，短所がある。計算（筆算）をするときにはインドの記数法はたいへん優れている。例えば365×27は次のように実行された。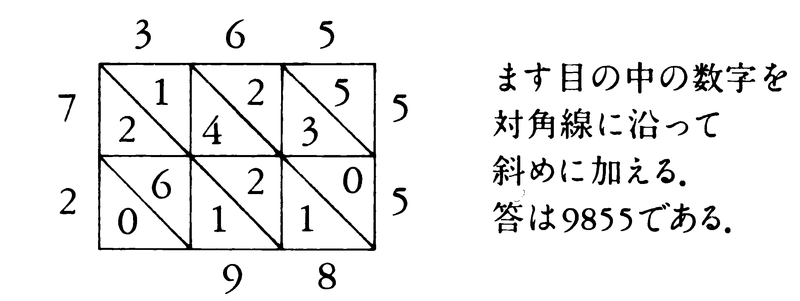

これを三百六十五×二十七と考えると，

とするしかない。前者のほうがはるかに簡単であり，位取りの原則が非常にうまく使われていることがわかる。ヨーロッパでインドの記数法が広く利用され始めたのは，人々が筆算をするようになって，そのよさが認められてからである。一方，1000000000001は漢字で書けば一兆一である。漢字で書くほうがはるかに読み取りやすく，また書きやすい。ギリシアのイオニア式記数法も同様な長所をもっている。

　1より小さい数を表すのにわれわれは十進小数を使っている。小数そのものは，メソポタミア，中国で古くから使われていたが，オランダのステフィン（ステビンともいう）Simon Stevin（1548-1620）は統一的に十進小数を使うべきことを主張し，それを広めた。彼は，〇で囲んだ数字で小数の位取りを示し，現代の21.4142を21⓪4（1）1（2）4（3）2（4）で表した（運算のときは，⓪（1）（2）（3）の位置を変えた）。これより以前に，ドイツのクリストフ・ルドルフChristoph Rudolff（1500ころ-45ころ）は複利表を出版し，その中で小数点に相当するものとして｜を利用して21.4142を21｜4142のように記した。
執筆者：丸山 正樹

図－記数法

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

記数法
きすうほう

数を書き表す仕方をいう。今日では、10個のアラビア数字0、1、2、……、9を用いた十進位取り記数法(じっしんくらいどりきすうほう)が用いられる。たとえば、324と数を表すとき、3は百の位を表し、100が三つあることを、2は十の位を表し、10が二つあることを、4は一の位を表し、1が四つあることを、それぞれ示している。このように、各数字が、どの位置にあるかによって、その示す大きさが定まってくるのが位取り記数法である。この記数法では、ある位が欠けているときは、そこになにもないことを示すための数字として、0が必要である。そして、これによって、どんな大きな数でも表せるし、小数点を使うことによって、0に近いどんな数でも表すこともできる。

　十進法でなく、二進法、十二進法、六十進法による位取り記数法によっても数を表すことができる。二進法のときは、0、1の二つの数字だけを使えばよい。たとえば、十進法で11と表される数は、二進法では1011と表す。

［三輪辰郎］

[参照項目] | 十進法 | 二進法

出典　小学館　日本大百科全書(ニッポニカ)

百科事典マイペディア

記数法【きすうほう】

数を数字で表現する方法。現用される十進法のほか，二進法，十二進法，六十進法等がある。一般にp進法（０，１，２，…，p−１のp個の整数を用いる）による表現をa(/n)a(/n)(/-)₁…a₁a(/0)（a(/n)〜a(/0)はそれぞれ０〜p−１のどれか）とすれば，その値は　a(/n)p(n/)＋a(/n)(/-)₁p(n/)(-/)¹＋…a₁p¹＋a(/0)→数
→関連項目数字

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

記数法
きすうほう

「数字と記数法」のページをご覧ください。

出典　ブリタニカ国際大百科事典 小項目事典