ダービン‐ワトソン比（読み）だーびんわとそんひ（英語表記）Durbin-Watson ratio

日本大百科全書(ニッポニカ)

ダービン‐ワトソン比
だーびんわとそんひ
Durbin-Watson ratio

計量経済学における線形回帰モデルについて、確率攪乱(かくらん)項に自己相関があるかどうかを検証する際に用いられる統計量のこと。線形回帰モデルに関する基本的な仮定の一つとして、確率攪乱項には自己相関が存在しないことが規定される。もし、現実に作成される線形モデルの確率攪乱項に自己相関が存在することになれば、推定される係数の値の信頼性に疑問が生ずることになり、作成されたモデルにおいて、なにか重要な説明変数が見落とされていたり、モデルの関数型に問題があることになる。このことを検証するために、推定された回帰方程式から得られる残差項etを用いて次の統計量を作成する。

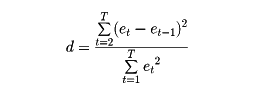
これがダービン‐ワトソン比とよばれるものであり、その値は、残差の系列に自己相関（一階の）が強くなるにつれて、正の相関のときは0に、負の相関のときは4に近づく。確率攪乱項に系列相関がまったく存在しないという仮説のもとでのダービン‐ワトソン比dの厳密な分布型は、自由度や説明変数の数、さらに説明変数の観測値の状態によっても変動する。そこで、J・ダービンとG・S・ワトソンは、系列相関0の仮説のもとでの分布について、特定有意水準に対する下側パーセント点の下限d_Lと上限d_Uの数値を作成した。モデルについて計算されたdと仮説との関係は、d＜d_Lならば仮説は棄却され（すなわち、系列相関が存在するということ）、d＞d_Uならば仮説は棄却されない（すなわち、系列相関不存在との仮説はいちおう維持される）ということになる。しかしd_L＜d＜d_Uの場合には、dの分布が説明変数の観測値に影響されるために、系列相関の仮説については、なんらの結論も得られない。残差の自己相関が負であるときにはdの値は2より大となり、この場合にはdのかわりに4-dとして検定手続を行うことになる。

［高島　忠］

[参照項目] | 計量経済モデル | 自己相関

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

ダービン=ワトソン比 (ダービンワトソンひ)
Durbin-Watson's ratio

弾道学の分野で，砲弾の飛距離のばらつきに関するデータをより公正に処理するためフォン・ノイマンが1941年に提案した考え方（ノイマン比von Neumann's ratio）にヒントを得て，J.ダービンとG.S.ワトソンが他の分野での分析に適用できるように考案した（1950）もの。これによって線形回帰方程式の誤差項の系列相関の強弱が測定でき，同時に説明変数の欠落や関数形の不適合も判定できる。回帰方程式の計測に際しては，異時点の観察値の誤差項は無相関であると仮定されている。もし誤差項に系列相関があれば，ある時点の観測値の誤差の影響が将来時点にも及ぶ。たとえば経済成長率を予測する際に，ある年で過大推計を行えば，その年以降も過大推計が持ち越されるので，正しい予測が不可能になるのである。最小二乗法であてはめられた回帰式からの残差の平方和を分母に，残差の階差の平方和を分子にして計算し，ダービン=ワトソン統計表に照らし合わせて系列相関の検定をする。この値が2に近いほど系列相関なしと判定する。
執筆者：粟山 規矩

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

ダービン＝ワトソン比
ダービン＝ワトソンひ
Durbin-Watson ratio

線形回帰模型において攪乱項に自己相関があるか否かをテストするための統計量の一つで，1950年 J.ダービンと G.S.ワトソンにより提案され，また検定のための臨界値の表が与えられた。ダービン＝ワトソン比は通常記号 dで表わされ，dは一般に (0，4) の範囲の値をとり，攪乱項に正の自己相関があると0のほうに近く，負の自己相関があると4のほうに近い値をとる。

出典　ブリタニカ国際大百科事典 小項目事典