日本大百科全書(ニッポニカ) 「エルゴード性」の意味・わかりやすい解説
エルゴード性
えるごーどせい
ergodicity
物理においては、力学系の運動の長時間平均と位相空間における平均が一致する性質。統計力学は、物理量の熱平衡状態での値を物理量の長時間にわたる時間的な平均値の基礎と考え、それを位相空間での等エネルギー面での平均値とする。長時間平均が、位相空間での等エネルギー面での平均値と等しいためには、等エネルギー面全体をくまなく運動することが必要である。この性質のことをエルゴード性という。このような性質は一般的には証明されていない仮定なので、その理論はエルゴード仮説ともよばれる。1884年ボルツマンによって初めて使われた。この語は、ギリシア語のエルゴン(仕事)とオドス(道)に由来している。
位相空間の1点が運動するのはあくまで線上なので、多次元の等エネルギー面でくまなく運動するとはどのようなことであるかについて、準エルゴード性などの考え方の導入により理論が精密化され、数学的に詳しい議論がなされている。また、シナイYakov G. Sinai(1935― )によって二次元剛体球の例が示されている。また、熱平衡状態が実現されるためには、エルゴード性に加え、緩和機構に関する混合性などの条件が必要となる。調和振動子系などのようにエネルギー以外の保存量をもつ系ではエルゴード性は成り立たず、さらに弱い摂動に対しても位相空間に非エルゴード領域が残ることも知られている(KAM理論=コルモゴロフ・アーノルド・モーザー理論)。
エルゴード性は可逆な力学系の概念であるが、不可逆なプロセスを取り扱う場合にも、すべての状態間が遷移可能な場合にも、エルゴード性とよばれることがある。
[宮下精二]
エルゴード仮説は、数学的には測度論を用いることによってはっきりした形で論ぜられるようになった。次の定理は1930年代の初めにバーコフによって得られたものである。「集合Ωの上に完全加法的な測度m(m(Ω)<∞)が定義されているとする。またTはΩをΩの上に移す1対1の変換であって、Ωの任意の可測集合Eに対してm(E)=m(T(E))が成り立つとする。このときΩ上で積分可能な関数f(ω)に対して、極限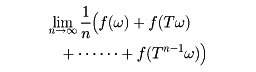
は、測度0の集合を除いて存在し、この極限をg(ω)と置けば、g(ω)=g(Tω)が測度0の集合を除いて成立し、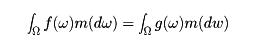
が成り立つ」。これをバーコフのエルゴード定理という。
次に完全加法的測度mが定義されている集合Ωの各点ωが時間の経過とともに動く場合を考え、点ωが単位時間の間に移る点をT(ω)と表したとき、この変換Tがバーコフの定理における条件を満たすものとする。またΩの任意の可測集合Aに対してm(T(A))=m(A)であればAは測度0の集合を除いて空集合またはΩと一致するものとする。この場合、バーコフの定理のg(ω)(これはf(ω)の長時間平均を表す)は測度0の集合を除いて定数値をとり、したがってバーコフの定理によってfの長時間平均と空間平均は一致することになる。
[古屋 茂]

