緩和現象（読み）カンワゲンショウ

デジタル大辞泉

かんわ‐げんしょう〔クワンワゲンシヤウ〕【緩和現象】

外的作用によって平衡状態の乱れた物質系が、内部運動によってしだいに平衡状態に戻る現象。

出典　小学館

精選版 日本国語大辞典

かんわ‐げんしょうクヮンワゲンシャウ【緩和現象】

1. 〘 名詞 〙 平衡状態を乱した時、次第にもとの平衡状態にもどっていく現象。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

緩和現象
かんわげんしょう

外界に囲まれている体系が熱平衡状態にあるとき、外界が急に変化すると、体系も変化（応答）し、新たな外的条件で決まる熱平衡状態に向かっていく。このような、外界の変化（作用）に対して、体系が新しい熱平衡状態になるのに時間がかかる現象を緩和現象という。たとえば、仕切り壁のある容器内の一方を占めていた気体が、仕切り壁に穴を開けると、真空に保たれた他方へ拡散し、やがて容器全体で一様な密度をもった気体になり、熱平衡状態になる。

　初め磁化をもたない磁性体に急に磁場をかけると、磁性体の磁化は徐々に増加し、やがて一定の磁化をもった磁性体になる。また誘電体（絶縁体）に急に電場をかけると、誘電体に電気分極がおきるときも同様な現象が生じる。これも新しい外的条件（磁場、電場）での新しい平衡状態への緩和現象である。金属のような導体に電場をかけると、即座に電流が流れ、電場を切るとすぐ電流が止まるようにみえるが、やはり緩和のある現象である。

　外場に対する応答が外場の大きさに比例するとき、線形応答とよばれる。一般に外場が小さいときは線型応答になるが、外場が大きいとき、応答が外場の大きさに比例するとは限らない。このときは非線形応答とよばれている。

［小野昱郎］

誘電体の緩和

誘電体の電場による電気分極の変化を考えてみよう。始め電場E＝0では分極が0で、時刻t＝0で、急に電場Eが加えられたとしよう。そのとき分極の時間変化をP(t)で表すと、始め0であった分極P(t)は電場E下での平衡値P_eq(E)にしだいに近づく。これを図Aに示す。また逆に電場中に置かれた誘電体の電場を急に切ると、分極はP_eq(E)の値から0に緩和する。これを図Bに示した。これを式で表すと、電場を急にかけたとき、
　　P(t)＝P_eq(E)(1－e^-t/τ)　　(1)
また電場を急に切ったとき
　　P(t)＝P_eq(E)e^-t/τ　　(2)
となる。したがって、いずれの場合も分極は新しい熱平衡値に向かって指数関数的に緩和することになる。これをデバイ緩和といい、τ(タウ)は緩和時間とよばれている。このような緩和の仕方は多くの物理現象に共通にみられるものである。

　電場Eをかけたとき、分極P(t)の時間変化が次の微分方程式に従うとしよう。

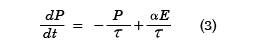
　ここで、α(アルファ)は定数である。十分時間がたったときは、P(∞)は一定の値になる。前記の式で

とおけば、P(∞)＝αEが得られる。この値は電場Eの下での分極の熱平衡値であるから、P_eq(E)＝P(∞)＝αEである。このことから、αは電気分極率であることがわかる。

　初期条件がP(0)＝0、t＞0でE≠0のとき、(3)の方程式の解は、(1)式で与えられることは容易に確かめられる。また、初期条件がP(0)＝αE、t＞0でE＝0とすれば、(2)式が同じ方程式の解であることもわかる。したがって、P(t)がデバイ型の緩和とすれば、その時間変化は(3)の方程式を満足することがわかる。

［小野昱郎］

金属電流のデバイ型緩和・吸収

電気の導体（金属）に電場をかけたときの電流の時間変化も同じようなデバイ型緩和を示す。金属中の電子の流れは衝突によって減衰するから、電子による電流も同じように減衰する。デバイの緩和時間をτとすれば、電場E中での電流j(t)は

のように、分極と同じような時間変化をすると考えられる。ここで、σ(シグマ)は電気伝導率である。電流の定常値は
　　j_eq(E)＝σE
と与えられる。これはオームの法則である。

　以下では振動する電場をかけたときの応答を考えてみよう。外部より与えられた振動電場をE(t)＝E₀cos(ωt)のように表すと、定常振動電流j(t)は同じ振動数で振動するが
　　j(t)＝j'(ω)cos(ωt)
　　　＋j"(ω)sin(ωt)　　(5)
のように外場と同じ位相で振動するj'(ω)の成分と90度ずれた位相で振動するj"(ω)の成分をもつ。この式を(4)式に代入して解けば、

が得られる。単位時間当りのエネルギー吸収率はW(t)＝j(t)E(t)であるから、1周期で平均をすれば、同位相で振動する成分j'(ω)のみが吸収に寄与することがわかる。その値は

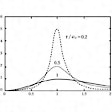
である。図Cに吸収の強度の振動数依存性を示す。これを吸収型またはデバイ型吸収曲線という。

［小野昱郎］

ローレンツ型緩和・吸収

単振動で速度に比例した抵抗力による減衰がある系の場合を考えてみよう。振動する外力のもとで定常的に振動がおこっているとき、急に外力を止めると、デバイ型のように単純に減衰するのではなく、振動しながら減衰していくことがわかる。これを共鳴型緩和とよぶ。

　共鳴振動数ω₀をもつ減衰振動する系で、減衰項が－mγvで与えられるとしよう。ここで、mは物体の質量、vは速度である。このような系では、振動外力f(t)＝f₀cosωtによるエネルギーの単位時間当りの吸収率は、v(t)f(t)に比例し、その時間平均はデバイ型と異なり、外力と同じ位相で振動する変位xの応答成分ではなく、90度ずれた応答成分に比例する。その形は

で表される。ここで、f₀は外力の大きさである。この吸収曲線の外場による振動数依存性を図Dに示す。デバイ型と違って、共鳴振動数ω₀に吸収のピークがあることがわかる。これを共鳴型またはローレンツ型吸収曲線という。このように緩和時間を緩和関数から直接求めなくても、振動外場に対する吸収曲線の幅から決めることもできる。

［小野昱郎］

多種の緩和型

一般に外場やゆらぎで物理量Pが熱平衡値からすこし外れた値ΔP＝P－P_eqをもったとき、平衡値へ自然に緩和する（戻る）場合、

の方程式に従うとすれば、デバイ緩和になることがわかる。

　熱平衡からすこし外れた状態から熱平衡に近づく平衡緩和のときデバイ緩和になることが多いが、緩和時間が一つでは記述できないこともある。また臨界点に近い場合とか、スピングラス転移では緩和はデバイ型でなく、べき型t^-sや、対数型logtのような形で緩和することもある。

［小野昱郎］

緩和関数（誘電体に急に電場を加えたとき…

緩和関数（電場を急に取り去ったときの分…

デバイ型緩和の吸収曲線の振動数依存性〔…

ローレンツ型緩和の吸収曲線の振動数依存…

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

緩和現象 (かんわげんしょう)
relaxation phenomenon

ある外的条件の下で平衡状態（あるいは定常状態）にある物質系で，外的条件を急に変化させると，系の状態は新しい条件の下での平衡状態に遷移していく。その遷移は瞬間的なものとは限らず，むしろ時間の経過とともに徐々に変化していき，最後に一定の平衡状態に達する。すなわち，外的条件の変化に対して系の状態が新しい外的条件の下での平衡状態に達するまでには遅れが存在する。このような遅れの存在する現象を緩和現象といい，遅れの目安となる時間を緩和時間と呼んでいる。ただしこのような現象はあまりにも一般的なものであるため，遷移に要する時間が非常に短くて問題にならない場合や，逆に非常に時間がかかる場合は緩和現象の範疇（はんちゆう）に含めないのがふつうである。言い換えれば緩和現象では遷移の過程そのものが重要な意味をもっているといえる。

　緩和現象は多くの場合，ある観測時間の範囲では，Q（t）＝｛Q（0）－Q（∞）｝exp（－t/τ）＋Q（∞）の形で表される。ここでQ（0）は時間t＝0のときの，またQ（∞）はt＝∞のときの系の状態を表している。この式は線形微分方程式dQ（t）/dt＝－｛Q（t）－Q（∞）｝/τの解であり，このような形で表される場合を線形緩和と呼んでいる。τは変化が1/eだけ進行するのに要する時間を表しており，このτを緩和時間と呼ぶ。緩和時間は考えている系の粒子間の相互作用によって決まる物理量で，その系の変動を表す重要な指標になる。なお，ここで述べたのはただ一つの緩和時間を用いて表せる場合であって，線形緩和でも多くの緩和時間を用いなければ記述できない現象や，線形緩和以外の非線形緩和と呼ばれる現象も多い。

　緩和現象という概念は，19世紀の後半，J.C.マクスウェルによって粘弾性体の外力による変形を説明するために導入されたもので，その後1929年，P.デバイによって双極子の誘電緩和理論が発表されるに及んで，緩和現象が自然の非平衡状態を理解するのに基本的であることが認識されるようになった。非平衡系の物理量は，緩和時間と密接な関係にあり，この意味で，緩和現象は，物性物理学の多くの分野で非常に重要な役割を果たしている。

緩和現象の例

（1）誘電緩和現象　電気双極子モーメントをもつ分子からなる物質に，外部から電場を加えると電気分極を生ずる。これは電場によって双極子モーメントをもった分子が電場の方向に配向するためであるが，平衡状態に達するまでには有限の時間を要する。電場を変化させたり，取り去る場合も同様で，このような現象を誘電緩和現象と呼ぶ。緩和時間は電気双極子間の相互作用で決まり，この緩和時間を用いて誘電率が表される。この場合，実際上重要になるのは外部電場が一定の周期で振動する場合であって，このとき誘電率は複素数の形で与えられ，その虚数部分は，電場のエネルギーが物質に吸収され熱となって拡散する誘電損失を表す。

（2）磁気緩和　物質の磁化が，外部の磁場の変化に対して新たな平衡状態になるまでに有限の時間を要する現象。常磁性を示す物質は，古典的に考えれば，磁気モーメントをもつ分子の集団とみなしてよいから，一定の周波数で振動する磁場の下では帯磁率は誘電緩和の場合の誘電率と同様に複素数で与えられ，その虚数部分は，単位体積の試料が単位時間に吸収するエネルギーを表す。帯磁率，または緩和時間をミクロに議論するためには，磁性の根源となっている電子のスピンどうしの相互作用やスピンと格子との相互作用を考慮しなければならない。磁場が弱いときは10⁻¹⁰秒ぐらいの短い緩和時間で，スピン間の相互作用によって新しい定常状態に達するが，磁場が強くなるとスピンと格子との相互作用によってもっと長い緩和時間（10⁻¹⁰～10⁻⁶秒）で緩和する。
→磁気緩和
（3）電気伝導　電気伝導も緩和現象の重要な例である。金属内の電気伝導に関係する電子は，電場が作用していないときは，ふつうの熱平衡状態（フェルミ分布）にある。これに電場が作用すると，負の電荷をもつ電子は，電場と反対方向に平均として0でない速度をもつようになって全体として電流が流れることになる。電流Jは電場Eを用いてJ＝σEと表される（σは電気伝導度）。電子の自由行程時間（緩和時間）τを用いると，近似的に，と表される。ただし，Nは電子密度，mは電子の質量，eは電子の荷電量である。上式は，電場Eの中の電子はローレンツ力によってeE/mの加速を受け，τの時間にτ（eE/m）の速度になることから直観的に導かれる。

（4）臨界緩和　相転移が起こる物質では，その相転移点近傍になると，分子密度，磁化密度などのゆらぎが非常に大きくなるため，緩和時間τが異常に大きくなり発散することが多い。これを臨界緩和という。いちばん簡単な近似理論（分子場理論）によると，τは転移点T_c近傍で，τ∝（T－T_c）⁻¹のような異常性を示す。
執筆者：鈴木 増雄

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

緩和現象
かんわげんしょう
relaxation phenomenon

物理系や化学系に作用する外的条件が変化したとき，それに応じる系の応答がただちに現れず徐々に進行するという現象。系がある外的条件のもとで平衡または定常な状態にあるとき，急に外的条件を変えると，系は新しい平衡または定常な状態に向って変化していくが，この過程には一般に有限な時間を要する。この緩和現象が時間 t に対して exp (－t/T) の形で進行するとき，定数 T を緩和時間または時定数，1/T を減衰定数という。系が最終状態に達するには，数学的には無限の時間を要するが，実質的には T の数倍程度の時間で最終状態になったとみなしてよいから，緩和時間 T はその進行の速さの目安となる。緩和に時間を要するのは，系内の粒子の間の相互作用に基づく慣性が変化を妨げるためである。たとえば，弾性体に対し弾性限度内の小さい応力を与えると，これを取除いても瞬間的にはもとの状態に戻らず，ある程度の時間にわたって弾性余効が残るのは緩和現象の例である。緩和現象には，外的条件を急にある値だけ変えて，その後は一定の値に保ち，これに対する物理量の時間的変化 (余効関数) を観測する静的な場合と，外的条件を周期的に変化させて，これに対する物理量の周期的変化 (応答関数 ) を観測する動的な場合とがある。

出典　ブリタニカ国際大百科事典 小項目事典

化学辞典 第2版

緩和現象
カンワゲンショウ
relaxation phenomenon

ある物質系を支配している外部条件が瞬間的に変化した場合，系は新しい外部条件で決まる平衡あるいは定常の状態に向かって変化するが，それは一般に，ある時間的遅れをもって到達する．この現象を緩和現象という．たとえば，ある回路系で，電場の強さ E₁(一定)を瞬間的にほかの強さ E₂(一定)にかえたとき，電流Iの時間的変化は次のように与えられる．

I(t) ＝ I₂＋(I₁ － I₂)e^－t/τ

ここで，I₁，I₂ はそれぞれ電場の強さ E₁，E₂ で決まる電流値，τは新しい平衡値に達するまでの目安となる時間(緩和時間)を示す．電場が周期的に周波数ωで振動する場合，

ωτ≫1
であれば電流はほとんど変化を受けない．一方，

ωτ ≅ 1
であると電流に顕著な異常が現れ，興味ある研究課題となっている．

出典　森北出版「化学辞典（第2版）」