フラクタル（その他表記）fractal

デジタル大辞泉

フラクタル（fractal）

部分と全体とが同じ形となる自己相似性を示す図形。
[補説]破片・分割の意のラテン語からの造語。

出典　小学館

精選版 日本国語大辞典

フラクタル

1. 〘 名詞 〙 ( [英語] fractal ) どのように分解してもその部分が元の全体と同じ形を備えていて、微分が不可能な図形。フランスの数学者マンデルブロー（B. B. Mandelbrot）がラテン語の fractas （破片・分割の意）をもとにつくった語。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

フラクタル
fractal

数学的な形の名称。自然の中にある形は，初等幾何学で教えられた正方形，円周，三角形などとは一見かけはなれたものが多い。例えば雲の形，リアス海岸線などはこれら初等幾何の図とはおよそかけはなれている。初等幾何のほうから円周を代表にとり，自然の形の代表としてリアス海岸線をとってみよう。まず円周は次のような特徴がある。全体としては曲がっているけれども，もしこれを細かい円弧に分解すると，十分細かく分解すれば，部分である円弧は線分とほとんど見分けがつかなくなる（つまり全体として曲がっているという性質が分解で失われていく）。一方，リアス海岸のほうは，岬や湾が無数に入りくんでいるが，これをいくつかの部分に分解してもなお，その部分では小さい岬や湾が入りくんでおり，全体がもっていた複雑さは部分になっても失われていない。円周の場合も現実にこれと寸分違わない形が存在するわけではなく，正多角形で内と外から近似し，それらの辺の数が無限になったときの極限としての理想化された曲線である。そこで海岸線のほうも理想化して，自己相似図形という数学的な図形を考える。全体はいくつかの部分に分解されるが，その部分は全体の縮小像であり，さらに，この分解にはいくらでも細かいものがあるようになっているときそれを自己相似図形と呼ぶ。もっとも簡単な例は線分であって中央から半分ずつに分解すると，それぞれはもとの線分の縮小像である。この操作をそれぞれの部分で行えば，1/4の縮小像が得られこの操作は無限につづけられる。もう一つの例はG.カントルの三進集合で，線分を3等分し，両端の二つの小線分を残すという操作を無限に行い，元の線分上に最後まで残っている点の集合である。さらに平面上の集合での簡単な自己相似図形はフォン・コッホH.von Kochが1906年に発見したコッホ曲線であって，その自己相似性は図を見れば明らかであろう。

　マンデルブローB.B.Mandelbrotは1967年ころに今まで述べたような自己相似図形やそれに関連した自己相似性をもつ図形をフラクタルと名づけ，コンピューターはこのような自己相似性をきわめて精度よく表現しうることを利用して，きわめて美しいフラクタルの数々を発表している。フラクタルという名は次に述べるハウスドルフ次元に関係してつけられている。すなわち，ハウスドルフF.HausdorffとベシコビッチA.S.Besikovičが1919年ころに発見したハウスドルフ次元というのは，上に述べた自己相似図形についてのみ説明してみれば，ふつうの次元，点は0次元，線は一次元，平面は二次元，立体は三次元というような位相的次元と異なって，非整数の次元も考えられるようにした別の次元なのである。先に線分は自己相似であるといったが，長方形も直方体も自己相似図形であって，それぞれN個の部分に等分すれば，相似比（部分/全体）は1/N，1/N^1/2，1/N^1/3である。一般にD次元の平行多面体ならば1/N^1/dである。そこで，一般的な自己相似図形が，つねに相似比rで分解されていることにすれば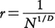，という式を対数を用いて，逆に解き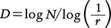，としてrからDをきめることにすれば，上の線分，長方形，直方体ではDは1，2，3となるが，前に述べたカントルの三進集合ではN＝2，r＝1/3でD＝0.6303，コッホの曲線ではD＝1.26……という非整数の次元が計算される。このことから分数（フラクション）の名をとってフラクタルと名づけたのである。
執筆者：山口 昌哉

図－フラクタルの例

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

フラクタル
ふらくたる

自然界には、たとえばリアス海岸の海岸線や、空に浮かぶ雲の形、河川の本支流の形、動物の体内に広がっている血管の分布の形、あるいは樹木の枝の形など、数学の初等幾何で扱う円や三角形、球、直方体などの整った形とは異なって不規則で複雑な図形が至る所に存在する。数学の古典的な微分法は、どんなに複雑なようにみえる形（曲線）であっても微分が可能である、つまり、全体としては曲がっていても、それを十分に細かく分解していけば、細分された部分はやがて直線と見分けがつかないほどになってしまう、いいかえれば十分に細分された微小部分は直線で近似的に表すことができる、という前提のもとに発展してきた。ところが前記のような自然界にみられる形はその図形を分解していって、その一部を取り出して拡大してみると、元の全体の図形と同じような複雑な図形を依然としてもっている。

　いま、どのように分解してもその部分が元の全体と同じ形を備えている図形を数学的に考える。このつねに元の形の縮小した形を備えているという性質を自己相似性という。自己相似性を備えた図形は、その微小部分が線分に近似できないから微分が不可能である。フラクタルとはそのような自己相似性を備え、どこでも微分が定義できないような形（集合）をいい、それを扱う数学をフラクタル幾何学という。

　このことばはフランスのマンデルブロB. B. Mandelbrot（1924―2010）がつくったもので、語源はラテン語のfractasであり、「破片」「分割」を意味する。

　フラクタルは定量的にはフラクタル次元（相似性次元）で表される。この次元は普通にいう一次元（線）、二次元（平面）、三次元（立体）といった整数で表される次元と異なり、非整数の値も含む次元であり、一般的には次元の高い図形のほうがより複雑で不規則な図形といえる。フラクタル図形は、現在、コンピュータで容易に描くことができ、コンピュータ・グラフィクスの分野で発展した観がある。事実、フラクタルは微分不可能であるため、コンピュータによる解析やシミュレーションが不可欠であり、コンピュータとともに発展した幾何学といえる。その対象には前記のような自然界のさまざまな形のほか、天体の分布、地震の発生頻度、ランダムウォーク、流体や高分子構造などきわめて広範囲であり、その研究と成果が注目される。

［栗原　裕］

『高安秀樹著『フラクタル』（1986・朝倉書店）』

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

フラクタル
fractal

自己相似性をもつ図形。地図上のリアス海岸線の形などのように，一部分を拡大すると元の図形と似た図形になる性質をもつ。フラクタルには，次のようにして，フラクタル次元という数が定義できる。一つの図形を大きさが r の N 個の要素（線分，正方形，立方体など）で覆い，r を小さくすると N と r^D が比例するとき，D をフラクタル次元という。フラクタルは，海岸線の長さの測定に関連して，ブノア・マンデルブローによって 1980年に提唱されたもので，これを基礎概念とした幾何学をフラクタル幾何学という。ちなみに，三陸海岸のフラクタル次元は約 1.35である。

出典　ブリタニカ国際大百科事典 小項目事典

化学辞典 第2版

フラクタル
フラクタル
fractal

1960年代にフランスの数学者Benoit B.Mandelbrotにより開拓された数学概念で，自己相似性を示す集合のこと．フラクタル集合Fは相似である各要素 F_i の合併集合であるが，F_i も同様に相似な要素に分解され，これが無限に繰り返される．たとえば，正三角形において各辺の二等分点を直線で結べば4個の正三角形ができる．中央の正三角形を除く残りの3個の正三角形に対して同様の操作を行い，この操作を無限に繰り返すと，入れ子構造の不思議な図形ができる(Sierpiński gasket)．これも一つのフラクタルである．複雑に入り込んだ多孔質物質の構造や，眺望した峰々の様子など，自然界にもフラクタルに似た図形が見られる．

出典　森北出版「化学辞典（第2版）」

百科事典マイペディア

フラクタル

1960年代の後半，米国IBM社のブノワ・マンデルブローが自己相似性という特殊な性質をもつ幾何学的図形に与えた名称。自己相似性とは，図形の全体をいくつかの部分に分解したとき，その各部分は全体の縮小図になっており，さらにこの分解の操作が限りなくつづけられることをいう。フラクタル図形が注目されるようになったのは，一つにはこのような自己相似性をもつ図形がコンピューターによりきわめて精度よく表現できることと，他方，自然界に現れる一見きわめて複雑な形であるリアス海岸線や雲の形などがフラクタル図形により近似できることが明らかになったことによる。

出典　株式会社平凡社

ASCII.jpデジタル用語辞典

フラクタル

樹木や雲、海岸線などの自然界にある複雑な形状を、同じパターンの図形で表す数学的概念。フラクタルによって描かれる図形は、全体像と図形の一部分が相似になる性質があり、このような性質を自己相似性と呼ぶ。自己相似性を持つものには、Benoit Mandelbrot氏が発見したマンデルブロー集合やコッホ曲線、ペアノ曲線、シェルピンスキー曲線、ドラゴン曲線、Levy曲線などがある。

出典　ASCII.jpデジタル用語辞典

知恵蔵

フラクタル

規模の尺度を変えても同じ形が現れる自己相似の構造。B.マンデルブローが名づけた。一例は樹木。幹の枝分かれは小枝の分岐にそっくりで、さらに葉脈の広がりにも似ている。山の稜線や海岸線などにも同様の構造がある。こうした輪郭の複雑さの度合いを表すのが、フラクタル次元。面上に描かれた輪郭は複雑になるほど1次元から2次元に近づく。

(尾関章 朝日新聞記者 ／ 2007年)

出典　(株)朝日新聞出版発行「知恵蔵」