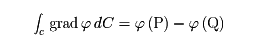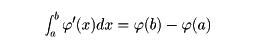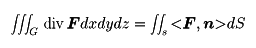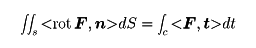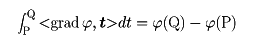改訂新版 世界大百科事典 「ベクトル解析」の意味・わかりやすい解説
ベクトル解析 (ベクトルかいせき)
vector analysis
ベクトル値関数の微分,積分などに関連する性質を扱うのがベクトル解析である。
ベクトルの微分と積分
例えば一つの質点が三次元空間の中を運動しているとき,その位置を表すベクトル r(x,y,z)は時間tの関数としてr=r(t)と表される。ベクトル値関数rの変数tに関する微分は,ふつうの実数値関数のときと同様に,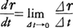
と定義する。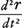 も同じように定義すると,
も同じように定義すると,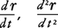 はそれぞれ運動する点の時刻tにおける速度ベクトル,加速度ベクトルを表す。ベクトル値関数A(t),B(t)および実数値関数λ(t)があるとき,積λA,スカラー積A・B,ベクトル積A×Bの微分についてはふつうの関数の積の微分の公式と同様に,
はそれぞれ運動する点の時刻tにおける速度ベクトル,加速度ベクトルを表す。ベクトル値関数A(t),B(t)および実数値関数λ(t)があるとき,積λA,スカラー積A・B,ベクトル積A×Bの微分についてはふつうの関数の積の微分の公式と同様に,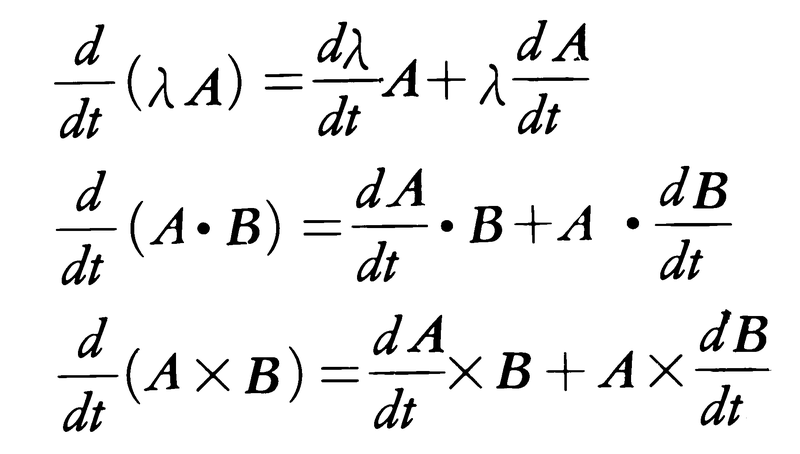
が成り立つ。A(t)がa≦t≦bにおいて連続のとき,その積分も実数値関数の場合と同様に定義する。すなわち,区間[a,b]の分割,
⊿:a=t0<t1<t2<……<tn⁻1<tn=bに対して,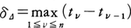
とし,tν⁻1≦sν≦tνなるsν(ν=1,2,……,n)をとって,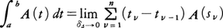
とする。ここでlimはδ⊿→0になるように分割を細かくしていったときの極限である。曲線に沿っての積分(線積分),平面あるいは曲面上での積分(面積分),空間領域における積分(体積分)についても,実数値関数の場合にならって同様に定義される。
スカラー場とベクトル場
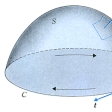
三次元空間内の領域Dの各点(x,y,z)にスカラー量φが与えられているとき,φをDで定義されたスカラー場という。またDの各点にベクトル量Fが対応しているとき,FをDで定義されたベクトル場という。例えばDの中で流体が流れているとき,Dの各点において流体の密度ρおよび流速のベクトルvが定まる。ρはスカラー場であり,vはベクトル場である。D内に曲線Cがあるとき,C上の各点でCの線要素ベクトルをdsで,その長さをdsで表し,ベクトル場Fのds方向の成分をFsで,また一般にFのx,y,z成分をFx,Fy,Fzで表すことにして,次の線積分を定義する。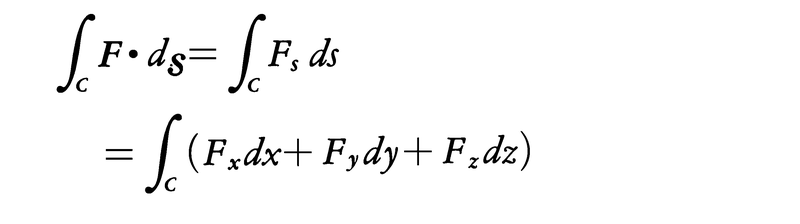
Cが閉曲線のとき,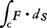 をFのCに沿う循環という。D内の曲面Sがあるとき,その面要素をdSと書くことにし,またS上の点における面要素ベクトルdSとは,方向がその点におけるSの法線nの方向で大きさがdSなるベクトルを意味する。S上の点でのベクトル場Fのn成分をFnと書くことにし,
をFのCに沿う循環という。D内の曲面Sがあるとき,その面要素をdSと書くことにし,またS上の点における面要素ベクトルdSとは,方向がその点におけるSの法線nの方向で大きさがdSなるベクトルを意味する。S上の点でのベクトル場Fのn成分をFnと書くことにし,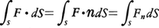
なる面積分を定義して,これをSを通過するベクトル流vector fluxという。
勾配,発散,回転
スカラー場φ(x,y,z)が与えられたとき,(∂φ/∂x,∂φ/∂y,∂φ/∂z)を成分とするベクトル場をφの勾配,あるいはグラディエントgradientと呼び,∇φ,またはgradφで表す。ベクトル場F=(Fx,Fy,Fz)に対して,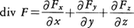 で定義されるスカラー場div FをFの発散といい,またx,y,z方向の単位ベクトルをそれぞれi,j,kとするとき,
で定義されるスカラー場div FをFの発散といい,またx,y,z方向の単位ベクトルをそれぞれi,j,kとするとき,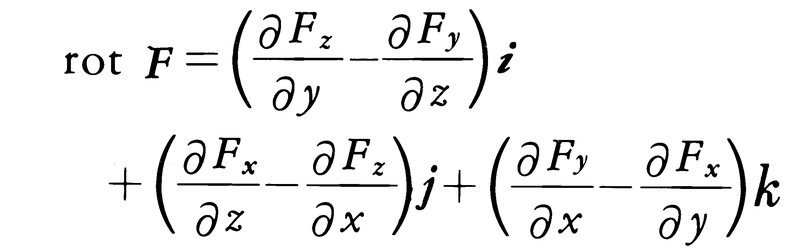
で定義されるベクトル場rot F(curl Fとも書く)をFの回転という。これらの演算に対して,rot gradφ=0,div rot F=0なる関係が成り立つ。ラプラス演算子Δを,
Δφ=∂2φ/∂x2+∂2φ/∂y2+∂2φ/∂z2で定義すると,任意のスカラー場φに対してΔφ=div gradφであり,また任意のベクトル場Fに対してその成分ごとにΔを作用させる演算をΔFと書くことにすると,
ΔF=grad div F-rot rot F
なる関係がある。空間内に閉曲線Cを縁(へり)にもつ曲面Sが与えられたとき,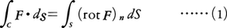
が成立する。これをストークスの定理という。また,閉曲面Sで囲まれた領域Vがあるとき,体積要素をdVと書くことにすると,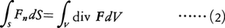
が成立する。これをガウスの定理という。Fが流速ベクトルのときは,(1)の左辺はCに沿う循環を表し,(2)の左辺はSを通って単位時間にVから流出する流量である。したがってrot F,div Fはそれぞれ流体の回転,わき出しを表しており,このことが,それぞれFの回転,発散と呼ばれる由来である。rot F=0のときベクトル場Fは渦なしであるという。このときFは局所的には,スカラー関数φを使ってF=gradφと表される。φをFのポテンシャルpotentialという。div F=0なるベクトル場Fはわき出しなし,あるいはソレノイダル(管状)であるという。このときFは局所的には,あるdiv A=0なるベクトル場Aを使ってF=rot Aと表される。AをFのベクトルポテンシャルvector potentialという。任意のベクトル場Fは局所的には,
F=gradφ+rot A (divA=0)
の形に,渦なしの場gradφとわき出しなしの場rotAとの和に分解される。これをヘルムホルツの定理という。
→ベクトル
執筆者:伊藤 清三
出典 株式会社平凡社「改訂新版 世界大百科事典」改訂新版 世界大百科事典について 情報


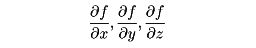
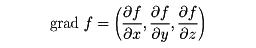
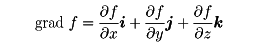
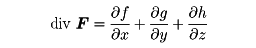
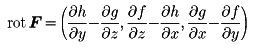
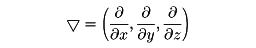
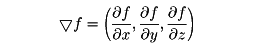
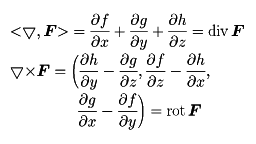
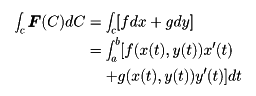
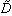 とすると
とすると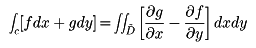
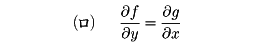
 ならば
ならば