二次体の整数論（読み）にじたいのせいすうろん（その他表記）arithmetic of quadratic fields

改訂新版　世界大百科事典

二次体の整数論 (にじたいのせいすうろん)
arithmetic of quadratic fields

1以外の整数mで，素数の2乗を約数としてもたないものによって，a＋b\(\sqrt{m}\)（a，bはともに有理数）の形で表される数の全体をQ（\(\sqrt{m}\)）で表し，\(\sqrt{m}\)で生成された二次体という。二次体Q（\(\sqrt{m}\)）においても，後述のように，有理数の場合と同様に〈整数〉が定義でき，整数論が展開できる。これを二次体の整数論という。二次体の整数論はC.F.ガウスに始まる。ガウスは，著書《数論研究Disquisitiones arithmeticae》において，整数係数の2変数の二次形式，

　aX²＋bXY＋cY²　（a，b，cは整数）

についての統一的な理論を構成した。この理論の大部分は，二次体の整数論として述べることができ，ここにおいて二次体の整数論の重要な部分が確立された。その後，P.G.L.ディリクレの解析的方法の応用や，J.W.R.デデキントのイデアルの理論などで，ガウスの理論がさらに進展し，二次体の整数論ができてきた。

　以下，二次体の整数論の基本的事項について述べる。

二次体の整数

二次体Q（\(\sqrt{m}\)）の2元α，βに対し，α±β，αβ，α/β（β≠0）もQ（\(\sqrt{m}\)）に含まれ，Q（\(\sqrt{m}\)）は体の例になっている。Q（\(\sqrt{m}\)）は，m＞0のとき実二次体，m＜0のとき虚二次体という。以下に述べるように，実二次体と虚二次体は，単数，類数などについて大きな違いを示す。

　Q（\(\sqrt{m}\)）の元αで，二次の項の係数が1の整数係数の適当な二次方程式の根になりうるもの，すなわち適当に整数a，bを選んで，

　α²＋aα＋b＝0

となるものをQ（\(\sqrt{m}\)）の整数という。以下，ふつうの整数をQ（\(\sqrt{m}\)）の整数と区別するため有理整数という。有理整数は整数であり，α，βが整数ならば，α±β，αβも整数であるが，α/βは整数とは限らない。Q（\(\sqrt{m}\)）の整数は次の形で与えられる。

（1）m≡1（mod 4）のときはa＋b\(\frac{1＋\sqrt{m}}{2}\)

（a，bは有理整数）の形の数。

（2）それ以外のときはa＋b\(\sqrt{m}\)（a，bは有理整数）の形の数。

Q（\(\sqrt{m}\)）の判別式Dを，（1）の場合D＝m，（2）の場合D＝4mと定める。 例えばQ（\(\sqrt{5}\)）の判別式は5，Q（\(\sqrt{－1}\)）の判別式はD＝－4である。

単数

整数αで，1/αも整数であるものを単数という。Q（\(\sqrt{m}\)）の単数全体をEで表すことにする。Eの構造は，虚二次体の場合は簡単で，D＝－3の場合はE＝｛±1，±ω，±ω²｝（ωは1の3乗根），D＝－4の場合はE＝｛±1，±i｝，それ以外はE＝｛±1｝である。実二次体の場合には単数は無限に存在し，それはある単数ε（ε＞1）によりE＝｛±εⁿ｜nは有理整数｝と表せる。このεを基本単数という。例えば，Q（\(\sqrt{5}\)）の基本単数は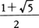である。

イデアルと類数

二次体の整数についても因数分解は考えられるが，素因数分解の一意性は必ずしも成り立たない。例えばQ（\(\sqrt{－5}\)）で6は，

　6＝（1＋\(\sqrt{－5}\)）（1－\(\sqrt{－5}\)）＝2×3

と二通りに分解される。この困難はイデアルという考えを用いてうまく処理することができる。Q（\(\sqrt{m}\)）の整数全体をΘで表すことにする。Θの部分集合Aが次の（1），（2）の性質をもつとき，イデアルであるという。

（1）α，β∈Aならばα±β∈A

（2）α∈Θ，β∈Aならばαβ∈A

αをΘの元とすると，（α）＝｛xα｜x∈Θ｝は（1），（2）を満たし，イデアルである。このように一つの元で生成されるイデアルを単項イデアルという。また二つのイデアルA，Bに対し，その積が，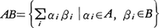

で定義される。素数に対応するものとしては，P≠Θであって，Θの元α，βに対し，αβ∈Pならばα∈Pまたはβ∈Pとなるものを考え，このようなPを素イデアルという。この素イデアルを用いると，Θと｛0｝以外のイデアルAは，の形に，適当な素イデアルP₁，……，P_nと正の有理整数e₁，……，e_nを用いて一意的に表される。

　｛0｝以外のイデアルA，Bが，Q（\(\sqrt{m}\)）のある元αによってA＝αBとなるとき，AとBが同じ類に属するものと定めて，｛0｝以外のイデアル全体を類に分けることができる。この類の数は有限で，これをQ（\(\sqrt{m}\)）の類数という。類数が1であることは，すべてのイデアルが単項イデアルであることと同じで，このとき整数は素因数の積に一意的に分解できる。類数を決めることは二次体の整数論では重要である。虚二次体のうち類数が1であるのは，D＝－3，－4，－7，－8，－11，－19，－43，－67，－163だけであることが知られている。実二次体の場合には類数1のものが無限に存在するであろうと予想されているが，まだわかっていない。

素イデアルと相互法則

二次体における素イデアルPは，Pに含まれる最小の正の有理整数をpとすると次の3種類に分かれる。

（1）（p）＝P

（2）（p）＝PP′，P≠P′

（3）（p）＝P²

（3）はpがDの約数の場合であり，pがDと互いに素のときは（1）または（2）となる。pが奇素数のときには，（1），（2）のどちらになるかは，平方剰余記号を用いて（\(\frac{D}{p}\)）＝1または－1で区別される。またイデアル（p）がどのように分解するかをさらに詳しく調べるのに，次のガウスによって証明された平方剰余の相互法則は重要である。

　定理　p，qが奇素数であるとき，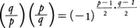

これを用いると，例えばP≡q（mod D）ならば，（p），（q）を割る素イデアルは（1），（2），（3）の同じ型に属することがわかる。
執筆者：斎藤 裕

出典　株式会社平凡社「改訂新版　世界大百科事典」

世界大百科事典（旧版）内の二次体の整数論の言及

【整数論】より

…ガウスはとくに平方剰余の相互法則に興味をもち，それぞれ異なった着想に基づく証明を全部で六つ与えた。その後ガウスは4乗剰余の相互法則の研究を始め，そのためにガウス数体と呼ばれる二次体の整数論を展開した。これが代数体の整数論の出発点となった。…

※「二次体の整数論」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」