代数曲線（読み）ダイスウキョクセン（英語表記）algebraic curve

デジタル大辞泉

だいすう‐きょくせん【代数曲線】

点の座標を未知数として、代数方程式で表される曲線。

出典　小学館

精選版 日本国語大辞典

だいすう‐きょくせん【代数曲線】

1. 〘 名詞 〙 点の座標を未知数とする代数方程式によって表わされる曲線。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

代数曲線 (だいすうきょくせん)
algebraic curve

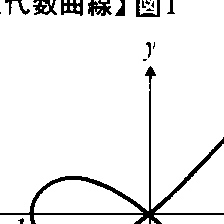
x²（x＋1）－y²＝0やx⁴＋y⁴－2x（x²－y²）＝0のように，既約な2変数多項式f（x，y）に対してf（x，y）＝0を満たす点（x，y）の全体を平面代数曲線（アフィン平面代数曲線）という。f（x，y）の次数がnのときn次曲線という。f（x，y）＝0で定義される平面代数曲線c上の点（a，b）は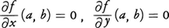，のとき特異点と呼ばれる。のときは正則点と呼ばれる。図1，2，3の平面曲線は原点が特異点であり，その他の点は正則点である。図1の特異点は通常二重点と呼ばれる。図よりわかるように通常二重点では異なる2本の接線（この場合はx－y＝0，x＋y＝0）を引くことができる。図2の特異点は尖点と呼ばれる。尖点では接線は1本しか引くことができない。一方，図3の特異点では3本の接線x＝0，x－y＝0，x＋y＝0を引くことができる。一般にf（0，0）＝0であれば，f（x，y）の次数のいちばん低い項をまとめたものをf₀（x，y）と書くと（図1の場合f₀（x，y）＝x²－y²，図2の場合f₀（x，y）＝y²，図3の場合f₀（x，y）＝－2x（x²－y²）である），このとき，f₀（x，y）の次数が1であれば原点は正則点，次数がm≧2であれば特異点であり，m位の特異点と呼ばれる。f₀（x，y）の一次因子ax＋byで定まる直線ax＋by＝0は接線になる。f₀（x，y）が相異なるm個の一次式の積であるとき通常特異点と呼ばれる。

　今日の代数幾何学では，通常は代数曲線は複素数や他の体のうえで考える。また射影空間の中で考えることが多い。代数曲線を解析的に取り扱うと閉リーマン面の理論になる。
執筆者：上野 健爾

図1～図3

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

代数曲線
だいすうきょくせん
algebraic curve

一次元（既約）代数多様体を代数曲線という。とくに、二次元複素空間C²のなかの代数曲線を平面曲線という。平面曲線Γは、ある二変数の既約多項式f(X,Y)をゼロにする点全体からなっている。つまり、Γ=｛(x,y)∈C²|f(x,y)=0｝で、このとき多項式fの次数を曲線Γの次数という。

　平面曲線Γの点P=(x,y)が
　　(∂f/∂X)(x,y)
　　　=(∂f/∂Y)(x,y)=0
を満たすとき、点PをΓの特異点という。特異点でない点で、曲線Γにただ1本の接線が引ける。Γの特異点は、存在したとしても、有限個しかないが、とくに特異点をもたないΓを滑らかな曲線という。

　定義多項式fでX、Yをそれぞれ、X/Z，Y/Zで置き換え、分母をうまく払って得られるX、Y、Zの同次多項式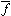で、二次元射影空間内に射影的代数多様体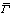が決まる。このような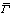を射影的平面曲線というが、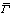はΓに無限遠点を加えたもので、代数関数論やリーマン面論で重要な役をする。

［菅野恒雄］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

代数曲線
だいすうきょくせん
algebraic curve

xy 平面において代数方程式 f(x，y)＝0 を満たす点 (x，y) 全体の集合を代数曲線といい，f(x，y)＝0 をその代数曲線の方程式という。 f(x，y) が n 次の2元多項式のとき，その代数曲線を n 次の代数曲線という。たとえば，アステロイドの方程式 x^2/3＋y^2/3＝a^2/3 は x，y についての6次の多項式 (x²＋y²－a²)³＋27a²x²y²＝0 に書き直せるので，6次の代数曲線であることがわかる。3次元の代数曲線は，2つの代数曲面の交わりとして表わしたものをいう。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の代数曲線の言及

【曲線】より

…曲線は極座標を用いてG(r，θ)＝0のようにも表すことができる。F(x,y)がx,yについての多項式のとき，F(x,y)＝0で表される曲線を代数曲線といい，多項式の次数がnのとき，これをn次曲線という。一次曲線は直線で，二次曲線は円錐曲線(楕円，双曲線，放物線および交わる2直線)である。…

※「代数曲線」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」