代数幾何学（読み）ダイスウキカガク（英語表記）algebraic geometry

デジタル大辞泉

だいすう‐きかがく【代数幾何学】

代数的に定義された多様体の性質を研究する数学の一分野。

出典　小学館

精選版 日本国語大辞典

だいすう‐きかがく【代数幾何学】

1. 〘 名詞 〙 代数曲線、代数曲面などを研究する数学の分野。古くは幾何学の一部門と見られていたが、現今では代数学の一部門と考えられている。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

代数幾何学
だいすうきかがく
algebraic geometry

n個の変数X₁、……、X_nの有限個の多項式
（1）　f_i(X₁,……,X_n)
　　　 　(i=1,……,r)
に対し、n次元複素線形空間Cⁿの点(x₁,……,x_n)で
　　f_i(x₁,……,x_n)=0
　　　(i=1,……,r)
を満たす(x₁,……,x_n)の全体の集合Vを、f₁,……,f_rで決まる代数多様体という。代数多様体を代数学や幾何学を用いて研究する学問を代数幾何学という。

　いま、前記のようなCⁿのなかの代数多様体Vがあるとき、多項式h=h(X₁,……,X_n)に対し、Vの点(x₁,……,x_n)をh(x₁,……,x_n)に写すVからCへの写像_hが得られる。このような写像全体C［V］=｛_h|h∈C［X₁,……,X_n］｝は、和と積を
　　_h+_g=_h+g,
　　_hg=_hg
とすると、可換環になる。この環C［V］をVの座標環という。とくにC［V］が整域のとき、Vを既約代数多様体という。

　Vが既約のとき、0≦d≦nなる整数で、次の2条件を満たすものが決まる。

（2）必要ならX₁、X₂、……の番号を付け直すと、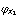,……,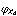はどんな多項式F(T₁,……,T_d)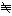0に対してもF(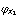,……,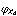)≠0であるが、
（3）d+1≦j≦nなるjに対しては、多項式G(T₁,……,T_d,T_d+j)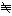0をうまくとると、G(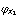,……,,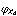 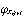)=0となる。

　このようなdを既約代数多様体Vの次元という。たとえばX₂²-X₁³+X₁で決まるC²内の代数多様体Vは既約で次元1である。またX₁ⁿ+X₂ⁿ-X₃ⁿ（n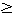3）で決まる二次元既約代数多様体Vが、座標が0でない整数になるような点をもつか、という問題は、有名なフェルマーの問題にほかならない。

　Cⁿから原点0=(0,……,0)を除き、0以外の2点(x₁,……,x_n)(y₁,……,y_n)がx_i=ty_i(t≠0)のように座標が比例しているとき、この2点を同じと考えたものをn-1次元射影空間P^n-1(C)という。

　（1）のf_iが同次式のとき、P^n-1(C)の点でf_iをゼロにする点全体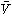を射影的代数多様体という。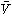は、代数多様体を有限個糊(のり)付けしたものでコンパクト位相空間に似ており、美しい理論が完成している。

　さらに最近、代数多様体の部分多様体全体を考えて生まれたスキームの理論にみられるように、現代の代数幾何学は、大きな規模をもって発展しつつ、他の数学分野にも応用されている。

［菅野恒雄］

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

代数幾何学 (だいすうきかがく)
algebraic geometry

歴史的には解析幾何学と射影幾何学が発展してできた分野であり，そのもっとも簡単な場合として有限個の多項式の共通零点として定義される図形の研究がある。例えば2変数n次既約多項式f（x，y）の零点f（x，y）＝0で定義される図形はn次（アフィン）平面代数曲線と呼ばれ，n＝1であれば直線，n＝2であれば二次曲線と呼ばれ楕円や放物線はその例である。

　N.H.アーベル，C.G.J.ヤコビによる楕円関数論の建設を経て，G.F.B.リーマンによる代数関数論の建設によって代数幾何学という新分野が生まれた。リーマンは代数曲線f（x，y）＝0を考察する際，複素数の範囲で考えた。すなわち，f（a，b）＝0である複素数の組（a，b）全体を考え，さらにこれに無限遠点をいくつかつけ加えて閉じた曲線として考察した。リーマンの導入したたいせつな概念に双有理変換がある。有理式R₁（x，y），R₂（x，y）を使って，u＝R₁（x，y），v＝R₂（x，y）によって（x，y）平面から（u，v）平面への変換（有理変換）を定めると，（x，y）平面の代数曲線f（x，y）＝0は（u，v）平面の代数曲線g（u，v）＝0に変換される。一般に二つの代数曲線f（x，y）＝0とg（u，v）＝0とが互いに有理変換できるとき，これらの曲線は双有理同値であるという。例えば直線y＝axと二次曲線u²＋v²＝1とは，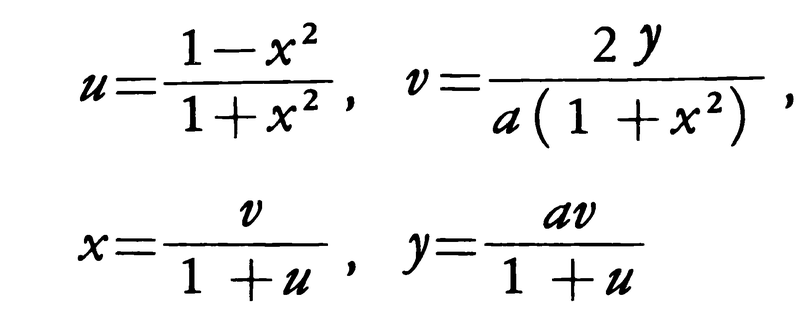

によって双有理同値である。しかし，y＝axとu²＝v³＋1とは双有理同値ではない。双有理変換によって平面曲線の次数は必ずしも不変ではなく，解析幾何学で平面曲線の次数がたいせつであったのとは著しい違いを示す。リーマンは双有理変換で不変な量として代数曲線の種数を導入した。上の例ではy＝axやu²＋v²＝1の種数は0であり，u²＝v³＋1の種数は1である。

　リーマンの考察は解析的であったが，彼の理論を代数的，幾何学的に再構成し，代数曲線論と呼ぶのにふさわしくしたのはM.ネーターであった。ネーターはさらに代数曲面をも考察し，彼の研究はF.エンリケス，G.カステルヌオーボらのイタリア学派に引き継がれ，20世紀前半に代数曲面論が建設された。一方，こうした代数幾何学の発展に伴って，体の理論や可換環論の発展が促された。イタリア学派の代数幾何学は直観に頼る部分が多く，その厳密な基礎づけは，体論，可換環論を使ってO.ザリスキ，A.ベイユによってなされ，現代の代数幾何学の発展の基礎をつくった。

　代数幾何学では射影空間の中で議論することが多い。射影平面内のm次代数曲線F＝0とn次代数曲線G＝0（多項式F，Gは既約とする）とは重複度をこめて数えれば，ちょうどmn個の点で交わる（ベーズの定理）。通常の空間（二次元アフィン空間）ではm次曲線とn次曲線の交点の数はmn個以下であり，mn個より真に少ない場合がある。こうしたことからも射影空間の中で考えることが便利であることがわかる。
執筆者：上野 健爾

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

代数幾何学
だいすうきかがく
algebraic geometry

射影幾何学を研究する一つの手段から，19世紀の初めに独立の地位を得た数学の一分科で，多元多項式の関係，あるいはその共通零点として表わされる代数的多様体を幾何学的構造によって記述する学問である。代数幾何学は一般に，まず体の上の射影空間を定義し，次に代数多様体を定義するのが普通である。この場合の体は任意の代数的数体でよいが，一般には可換体，代数的閉体，標数が0の体などといった条件がつけられた体である。特にこの体が複素数体である場合が，最近までのいわゆる古典的代数幾何学の研究対象であった。有限体の上の代数幾何学は，整数論との関係が特に深い。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

代数幾何学【だいすうきかがく】

高次元空間においていくつかの代数方程式で定められた点集合（図形）を扱う数字。20世紀半ばに体系的に整備されだし，20世紀でもっとも活発な研究分野となった。日本のフィールズ賞受賞者である小平邦彦，広中平祐，森重文も代数幾何学の研究者である。

出典　株式会社平凡社

世界大百科事典（旧版）内の代数幾何学の言及

【幾何学】より

…そこでは二次微分形式，複素構造，接続のような構造の与えられた微分可能多様体の理論が研究され，とくに微分幾何学的性質と位相幾何学的性質との関連を調べる研究が主潮になっている。なお，二次曲線や二次曲面を一般化して，高次元空間においていくつかの代数方程式の共通解の集合を代数多様体と呼び，これを研究する数学を代数幾何学と呼ぶが，これはおもに代数学を手段として用いるので，代数学の分野に属する。現在では，多くの数学が多様体を舞台として展開されていて，幾何学は数学全般に浸透し，代数学や解析学と有機的に関連して発展している。…

【数学】より

…それを多変数の場合に拡張することは20世紀にもちこされた。多変数代数関数論の幾何学的表現と見られる代数幾何学は19世紀後半イタリアで盛んに研究されたが，厳密性には欠けていた。それを基礎づけることも20世紀の課題となった。…

※「代数幾何学」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」