合同（読み）ゴウドウ（英語表記）congruence

デジタル大辞泉

ごう‐どう〔ガフ‐〕【合同】

［名］(スル)独立している二つ以上のものが一つになること。また、一つに合わせること。「二社が合同して計画した事業」「日中合同登山隊」
［名・形動］数学で、二つの図形が重ね合わせることのできる関係にあること。図形Aと図形Bが互いに合同であるとき、記号≡を用いてA≡Bと書き表す。「合同な三角形」
[類語]合併・合体・連合・同盟・連盟・合一・併合・合流・共同・協同・連携・提携・連名・共有・共用・催合もやい・タイアップ・協力・協賛・参与・チームワーク・共催・関与

出典　小学館

精選版 日本国語大辞典

ごう‐どうガフ‥【合同】

1. 〘 名詞 〙
2. ① 二つ以上のものが一つに合わさること。また、一つに合わせること。帰一。
   1. [初出の実例]「父子兄弟子孫臣妾みな相和睦して、和気合同(ガウドウ)するゆへに」(出典：翁問答（1650）上)
   2. [その他の文献]〔礼記‐楽記〕
3. ② 二つの図形の関係の一つ。図形Ａを移動によって図形Ｂに重ね合わすことができるとき、ＡはＢに合同であるといい、A≡B と書き表わす。全等。〔数学ニ用ヰル辞ノ英和対訳字書（1889）〕
4. ③ 二つの整数の関係の一つ。二整数ａ、ｂの差が、ある整数ｍで割り切れるとき、ａとｂとはｍを法（モデュラス）として合同であるといい、a≡b （modm）と書き表わす。たとえば一と四とは三を法として合同である。

出典　精選版 日本国語大辞典

改訂新版　世界大百科事典

合同 (ごうどう)
congruence

数学用語。

整数の合同

二つの整数a，bの差a－bが整数n（≠0）で割り切れるとき，aとbとはnを法（モデュラスmodulus）として合同であるといい，a≡b（modn）またはmodを略して，a≡b（n）と書く。例えば101≡2（11）である。a≡b（n），c≡d（n）ならば，a±c≡b±d（n），ac≡bd （n）であるので，法nを固定した場合，合同式は等式と同様に辺々加えたり，辺々掛けたりできる。また，cがnと素であれば，ac≡bc （n）からa≡b（n）がでるが，cがnと素でないときは，例えば2a≡2b（2n′）⇒a≡b（n′）のように，適当に法を変えたうえで，aとbとの合同式が得られる。

　合同式3x≡2（5）を考えると，x≡－1（5）が解になる。一般に整数係数の多項式f（x）によって，f（x）≡0（n）の形の合同式を考えたとき，それを満たすxの値を見つけることを，この合同式を解くという。

　ax≡b（n）の形の合同式は，aとnとが互いに素であれば必ずx≡c（n）の形の解がある。2x≡3（4）のように，aとnとに共通因数があり，bとnとが互いに素であるときは解がない。もっと一般に，aとnとの最大公約数dをとると，（1）dがbの約数でないときは，この合同式ax≡b（n）は解をもたない。（2）bがdで割り切れるときは，a，b，nをdで割った商を，それぞれa′，b′，n′とすれば，ax≡b（n）の解はa′x≡b′（n′）の解である。a′とn′とは互いに素であるから，解がある。この整数の合同は，整数係数の多項式の場合にも利用できる。ax²＋by＋c≡a′x²＋b′y＋c′（modn）は，aとa′，bとb′，cとc′がそれぞれnを法として合同というように，二つの整数係数の多項式f（x₁，……，x_m）とg（x₁，……，x_m）とがnを法として合同とは，各単項式ごとにその係数がnを法として合同のときと定める。すると，整数のときと同様に，

　f₁（x₁，……，x_m）≡g₁（x₁，……，x_m）（modn）

　f₂（x₁，……，x_m）≡g₂（x₁，……，x_m）（modn）

ならば，

　f₁（x₁，……，x_m）±f₂（x₁，……，x_m）≡g₁（x₁，……，x_m）±g₂（x₁，……，x_m）（modn）

　f₁（x₁，……，x_m）f₂（x₁，……，x_m）≡g₁（x₁，……，x_m）g₂（x₁，……，x_m）（modn）

が得られる。

　この合同の概念は，代数的整数の環や，もっと一般的な環におけるイデアルを法とする合同，あるいは，群において，部分群を法とする合同の概念にも一般化されている。

幾何学における合同

平面上の二つの図形F，Gについて，Fを動かして，Gに重ね合わすことができるとき，FとGとは合同であるという。ここで，動かすというのは，次の3種類の運動の組合せによるものをいう。（1）回転，（2）平行移動，（3）裏返し（折返し）。

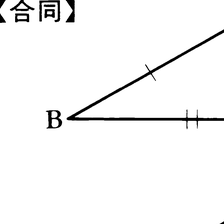
　FとGが合同であることを，F≡Gと書く。合同の内容を詳しくいい表すために，点P₁とQ₁，P₂とQ₂が対応して合同というように，対応する点，線分，弧などを述べたうえで，合同といういい方をすることがあるが，それはFをある動かし方でGに重ねるのに，対応するものが重なるようにできることを意味する。例えば△ABC≡△A′B′C′というとき，とくに断りがなければ，A，B，CがそれぞれA′，B′，C′に対応することを含めるのが通例である。この意味で，次の三つのおのおのは，△ABC≡△A′B′C′であるための必要十分条件である（図）。

（1）3辺の合同　AB＝A′B′，BC＝B′C′，CA＝C′A′

（2）2辺とその間の角の合同　AB＝A′B′，BC＝B′C′，∠ABC＝∠A′B′C′

（3）1辺とその両端の角の合同　BC＝B′C′，∠ABC＝∠A′B′C′，∠BCA＝∠B′C′A′

　1辺の長さが互いに等しい二つの正n角形は合同である。半径の等しい二つの円も合同である。この合同の概念は空間図形にも拡張される。

合同と同値関係

整数の合同はnで割った余りが等しいことであり，図形の合同は，位置は違うかもしれないが，図形としては同じと考えられる。したがって，いわゆる同値関係を満たす，

（1）a≡a（n）　　　　　（1）F≡F

（2）a≡b（n）ならば　　（2）F≡Gならば

　b≡a（n）　　　　　　G≡F

（3）a≡b（n），　　　　（3）F≡G，

　b≡c（n）ならば　　　G≡Hならば

　a≡c（n）　　　　　　F≡H

（1）（2）（3）は，それぞれ反射法則，対称法則，推移法則と呼ばれる。
執筆者：永田 雅宜

図－合同

出典　株式会社平凡社「改訂新版　世界大百科事典」

日本大百科全書(ニッポニカ)

合同
ごうどう

二つの図形の間の関係を表す用語の一つ。また、二つの整数の関係を表すときに用いられることもある。

［柴田敏男］

図形の合同

二つの図形の一方を移動することによって両者がまったく重なり合うとき、二つの図形は合同であるという。ここで、移動とは、平行移動、回転移動、線対称移動の3種の移動と、これらを繰り返してできる移動である。空間図形の場合には面対称移動がこれに加わる。

　平面図形の基本は三角形であるが、二つの三角形が合同となる条件は三つある。辺角辺の合同、角辺角の合同、辺辺辺の合同の三つである。

(1)辺角辺の合同とは、二つの三角形の対応する2辺とその挟む角がそれぞれ重なることで、二辺夾角(きょうかく)の合同ともいわれる。

(2)角辺角の合同は、対応する二つの角とその頂点の間の辺がそれぞれ重なることであり、三角形の内角の和は180度であるから、2角がそれぞれ等しければ残りの角も等しくなり、したがって、二角一辺の合同ともいう。

(3)辺辺辺の合同は、対応する3辺がそれぞれ等しいことで、三辺の合同ともいう。

　これらの合同条件を基礎として平面図形のいろいろな性質、定理が導かれる。平面幾何を公理的に構成するときには、三つの合同条件のうち、辺角辺の合同は公理の一つであり、他の公理も用いることにより残り二つの合同条件は定理として証明される。一方、面積や体積を考えるとき、「合同な二つの図形は等積である」ことが計量の一つの基礎である。二つの図形A、Bが合同であることを記号A≡Bで表す。

［柴田敏男］

整数の合同

一つの正の整数mを定めるとき、二つの整数a、bの差がmで割り切れるならば、この二つの整数はmを法として合同であるといい、記号でa≡b(mod.m)と表す。たとえば、2を法として考えると、偶数どうしは合同であり、奇数どうしも合同であるが、偶数と奇数は合同ではない。すなわち、2を法として互いに合同なものをまとめると、整数全体が偶数全体と奇数全体に分類される。また、3を法として考えると、整数全体は、3の倍数全体、3で割ったとき余りが1の整数全体、3で割ったとき余りが2の整数全体の3種類に分類される。一般に、正の整数mを法として考えるとき、mで割ったときの余りの種類を考えればわかるように、整数全体はm種類に分類される。整数についての合同は、整数の性質を考えるうえでの一つの基本的な概念である。また、この種の合同は多項式どうしの合同にまで一般化されている。

［柴田敏男］

出典　小学館　日本大百科全書(ニッポニカ)

ブリタニカ国際大百科事典 小項目事典

合同
ごうどう
congruence

初等幾何学，整数論などで使われる術語である。 (1) 初等幾何学での合同　2つの図形 F₁ ，F₂ が，運動によって，ちょうど重ね合せられるとき，F₁ ，F₂ は合同であるという。2つの三角形が合同になる条件は，(a) 1辺とその両端の角が等しいとき，(b) 2辺とそれらによってはさまれる角が等しいとき，(c) 3辺が等しいときである。 (2) 整数論での合同　2つの整数 a ，b があって，a－b が m で割切れるとき，a ，b は m を法として合同 (または，a は b に modm で合同) であるといい，記号で a≡b(modm) と書く。このような式を合同式という (→剰余類 ) 。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

合同【ごうどう】

（１）幾何学では，二つの図形A，Bを移動によって重ね合わすことができるとき，AとBは合同であるといい，A≡Bと書く。（２）整数論では，二つの整数a，bの差が整数mで割り切れるとき，aとbはmを法（モデュラス）として合同であるといい，a≡b（mod m）と書く。
→関連項目相似（数学）

出典　株式会社平凡社

普及版 字通

【合同】ごうどう

合一。

字通「合」の項目を見る。

出典　平凡社「普及版 字通」

世界大百科事典（旧版）内の合同の言及

【三角形】より

…(1)～(5)における3直線の交点をそれぞれ三角形の内心，傍心，重心，垂心，外心といい，これらを総称して三角形の五心という(図7)。二つの三角形において，次の(1)(2)(3)のいずれかが成り立つとき，これら二つの三角形は合同となる。すなわち，一方の三角形を動かして他の三角形の上に重ね合わすことができる。…

【整数論】より

…整数論は，それらの整数の性質についての研究から始まるが，後に理論の発展とともに研究対象も広がっていった。この項目では，前半において整数の整除，合同などに関する初等的理論である初等整数論について述べ，後半で整数論の歴史を述べる。
【初等整数論】

［整除］
　二つの整数a,b(b≠0)に対して，　a＝qb＋r　(0≦r＜｜b｜，｜b｜はbの絶対値)　を満たす整数q,rがただひととおりに定まる。…

※「合同」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」