四色問題（読み）ヨンショクモンダイ（英語表記）four-color problem

デジタル大辞泉

よんしょく‐もんだい【四色問題】

いかなる地図でも境界線を接する国々は4色で塗り分けられることを証明せよ、という数学の証明問題。1976年米国のW＝ハーケンとK＝アッペルが大型コンピューターで証明した。

出典　小学館

精選版 日本国語大辞典

よんしょく‐もんだい【四色問題】

1. 〘 名詞 〙 数学の証明問題の一つ。いかなる地図も境界線を接する国々は四色を用いて塗り分けられることを証明するというもの。一八四〇年メビウスによって提出され、一九七六年アメリカのＷ=ハーケンとＫ=アッペルが大型コンピュータを用いて証明した。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

四色問題（よんしょくもんだい）
よんしょくもんだい
four-color problem

どのような地図でも4色で塗り分けられるか否かを明らかにする問題。1852年にロンドン大学教授であったド・モルガンに、学生が「線で接する国を違う色で塗るとして、地図を塗るのに必要な色の最大数は4である」ということについての、ある証明が正しいかどうかを尋ねた。ド・モルガンは答えがわからず、当時の有名な数学者であり物理学者でもあったW・R・ハミルトンに問い合わせの手紙を書いた。これが四色問題の発端といわれている。質問した学生はのちに物理学者となったガスリーFrederick Guthrie（1833―1886）で、兄からこの問題の証明を聞き、その真偽をド・モルガンに尋ねたのであった。

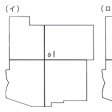
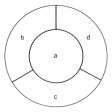
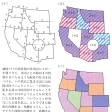
　地図では図A―(イ)の点aのように、色分けしたい国々（あるいは州など）の境界線がしばしば1点で交わることがある。しかしこの場合には、図A―(ロ)の灰色部のような架空の国を考え、この国も含めて色分けし、その色分けをそのまま図A―(イ)の点aの周りの国々の色として定めればよいので、国の境界はいつでも線で相隣るものと考えてよい。

　図Bのような地図はどの国も互いに隣り合っているから、4色が必要であることがわかる。したがって、問題はどんな地図でも4色あれば国々を塗り分けることができるか、すなわち、地図塗りには4色で十分であるか否かを明らかにすることであり、それが四色問題である。

　この問題は、1870年代後半にA・ケーリーが学会へ難問らしいと提唱してから、しだいに研究が進められるようになった。まず、1879年にケンペAlfred Bray Kempe（1849―1922）は「四色問題に関する地理学的問題」の論文を書き、これを証明した。この証明はその約10年後、ヒーウッドPeray John Heawood（1861―1955）が誤りを発見するまで正しいと思われていた。

　ケンペの考え方は数学的帰納法による。まず国の数が4個以下であればもちろん4色で十分である。国の個数がn個のときに4色で十分であると仮定してn＋1個の国の地図の場合、その国の数を減らす還元法を発見し、帰納法の仮定を用いてこの場合の証明をする、というものである。

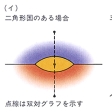
　この還元法を、たとえば地図に図C―(イ)のように二角形や三角形が現れる場合について考えてみる。これらの場合、二角形、三角形を無視して、たとえば図C―(ロ)のような地図について塗れば、最大3色で塗れるから、残りの1色を二角形、三角形に割り当てることによって4色で塗れる。よって二角形、三角形の国が現れれば、その地図は還元できることがわかる。

　図C―(イ)のように地図が与えられたとき、それを平面グラフとみて、その双対グラフを考える。つまり各国の中に新しく一つの頂点をとり、隣接する国の2頂点をその境界線と交わるような辺で結んでできるグラフを考える。この双対グラフは平面グラフであるが、頂点が国を表しているし、また各国は辺で接しているから二角形、三角形の場合と同様に処理して、双対グラフの面は三角形のみであると考えられる。よって双対グラフのほうが元の地図より四色問題としては扱いやすい。この双対グラフの頂点から辺がn本出ているとき、その頂点をn枝点という。n＝1,2の場合は前の二角形、三角形の場合であるから還元して除いてしまう。すると頂点はすべてn≧3に対するn枝点となる。n枝点の総数をVnで示すと、オイラーの多面体の公式から
3V₃+2V₄+V₅-V₇-2V₈-……=12
となる。この式の右辺は12＞0であるから、左辺のV₃,V₄,V₅の少なくとも一つは正である。すなわち、3枝点か4枝点か5枝点のどれか一つは少なくともどの双対グラフにでも現れる。

　よって、3枝点、4枝点、5枝点について還元法を発見すればよい。ケンペはそれを発見したつもりであったが、五枝点の処理が不十分であった。これを修正するのに多くの数学者が約100年間もさまざまな努力をしたのである。

　ヘーシュHeinrich Heesch（1906―1995）は1936年ころより40年間、その一生のほとんどをこの問題の解決に尽くし、よい結果を得ていたが、決定的な解決はアメリカのイリノイ大学にいるその弟子のハーケンWolfgang Haken（1928―2022）とその協力者アッペルKenneth Appel（1932―2013）によって1976年に与えられた。5枝点以上の還元は、複雑で、膨大な数の場合に分かれるが、アッペルとハーケンは4年間をかけて三つの別々の計算機を用いて千数百時間の計算時間を費やし、ようやくそのすべての場合について還元可能であることを実証したのである（計算機使用料は正規に払うと10万ドルを超えるといわれる）。

［野口　廣］

『一松信著『四色問題』（1978・講談社）』

[参照項目] | ド・モルガン | ハミルトン

四色問題説明図〔図A〕

四色問題説明図〔図B〕

四色問題説明図〔図C〕

四色問題（4色に塗り分ける手順の例）

四色問題（ししょくもんだい）
ししょくもんだい

→四色問題

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

四色問題 (ししょくもんだい)
four colour problem

四色（よんしよく）問題ともいう。平面上または球面上に描かれた地図の国を色分けすることを考える。ここに，どの国も飛地をもたずつながっているものとし，また海も一つの国とみなすものとする。もちろん相隣る国には異なる色を使うが，2国の境が有限個の点である場合は同じ色を塗ってもよいとする。このようにするとき，〈平面上または球面上に描かれたどんな地図も4色だけで塗り分けできるであろう〉というのが四色問題である。3色以下では塗り分けられないような地図は容易に作れるし，実際にやってみると，国の数を多くしても，また国の配置を複雑にしても4色で足り，5色以上が必要となる地図がなかなか作れない。こういう経験的事実から上の予想が生まれたのである。A.F.メービウスは1840年にこの予想を数学化して証明するという問題を提出したといわれているが，有名になったのは79年にA.ケーリーがロンドン地理学協会でその困難さを指摘してからである。それ以来，四色問題は問題そのものが簡単でだれにでもわかりやすいところから多くの人びとの関心を呼び，証明のための努力がなされた。そして90年にはヒーウッドP.J.Heawoodによって5色あれば色分け可能であることが示され，1937年にはフランクリンP.Franklinによって国の数が36以下であるときは4色で十分であることが示されたが，本質的な進展はみられず，永い間難問とされていた。しかしながら，76年になってこの難問も大型コンピューターの使用によりアッペルK.AppelとハーケンW.Hakenにより肯定的に解決された。彼らは地図の色分け問題は型の異なる1936個の標準的な地図の色分け問題に帰着できることを示し，コンピューターの使用により標準的な地図はいずれも4色で塗り分けられることを確かめたのである。このようにして，とにかく四色問題は解決されたのであるが，トーラス（浮輪の表面）上に描かれた地図については，7色で色分け可能で，それ以下では色分けできない地図の存在することが比較的容易に証明できる。
執筆者：中岡 稔

図1～図2

四色問題 (よんしょくもんだい)

→四色問題（ししょくもんだい）

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

四色問題
よんしょくもんだい
four-colour map problem

1850年代初めに提出された位相幾何学（→トポロジー）に関する問題。地図の隣り合った領域，すなわち共通の境界線をもつ領域が，同じ色にならないように塗り分けるには，最低何色の色が必要かという問題である。3色では足りないことは，実際に 3色では塗り分けられない 4個の領域からなる地図を描くことによって容易に示すことができる。地図の業者などの間では，古くから 4色で十分であることが経験的に知られていたようである。1879年イギリスの弁護士アルフレッド・ブレイ・ケンプが発表した論文の議論に基づいて，どのような地図も 5色で塗り分けることができることが示された。トーラス（輪環体。ドーナツの表面の曲面）上に描かれた地図については，最低 7色が必要であることが知られている。四色問題は，双対的に考えると，平面グラフの辺で結ばれた頂点が互いに異なった色になるように彩色する問題と同値であり，位相幾何学およびグラフ理論の立場から研究されてきた。1977年にケネス・I.アッペルとウォルフガング・ハーケン率いるイリノイ大学の数学者のグループによってこの問題は解決された。アッペルとハーケンらは 1936通りの地図のリストをつくり，4色で塗り分けられない地図があるとしてもこれらのいずれかの場合に帰着されることを示し，結果としてすべての地図は 4色で塗り分けられることを証明した。この証明ではコンピュータが本質的に用いられた。四色問題に対してコンピュータを用いない証明を与える試みは今日もなされている。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

四色問題【ししょくもんだい】

平面または球面上のどんな地図も４色で塗り分けられるかどうかという問題。境を接する国は色を違えなければならないが，１点を共有するだけなら同じでもよい。1879年A.ケーリーが提出した古典的な位相数学の問題。現実には５色を要する図は知られず，また５色なら十分なこと，国数が36以下であるときは４色で十分なことが証明されていたが，一般的証明は1976年米国イリノイ大学のW.ハーケンとK.アッペルによって，コンピューターを使ってついに達成された。
→関連項目位相幾何学

四色問題【よんしょくもんだい】

→四色(ししょく)問題

出典　株式会社平凡社

世界大百科事典（旧版）内の四色問題の言及

【四色問題】より

…四色（よんしよく）問題ともいう。平面上または球面上に描かれた地図の国を色分けすることを考える。…

※「四色問題」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」