日本大百科全書(ニッポニカ) 「差分法」の意味・わかりやすい解説
差分法
さぶんほう
finite difference method
広い意味では、数表の形で表された関数(表関数という)の変化率を扱う技法をいい、狭い意味では、微分方程式を差分方程式で近似して解く方法をいう。
[戸川隼人]
差分(階差)
変数xと変数yの関係を
x1 x2 …… xn
y1 y2 …… yn
とする(すなわち、xiに対応する値がyi)とき
Δxi=xi+1-xi
Δyi=yi+1-yi
を(一階の)前方差分(差分は、階差または定差ともいう)といい、その比
Δyi/Δxi
を(一階の)前方差分商という。また
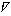 xi=xi-xi-1
xi=xi-xi-1
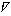 yi=yi-yi-1
yi=yi-yi-1
を(一階の)後方差分といい、その比
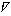 yi/
yi/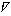 xi
xi
を(一階の)後方差分商という。xiが等間隔
xi+1=xi+h
(i=1,2,……,n-1)
の場合、
δyi/δxi=(xi+1-xi-1)/2h
を(一階の)中央差分商という。高階の差分は
Δkyi=Δk-1yi+1-Δk-1yi
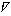 kyi=
kyi=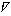 k-1yi-
k-1yi-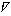 k-1yi-1
k-1yi-1
によって定義する。高階の差分商は、xiが等間隔ならば
(Δky/Δkx)i=Δky/hk
(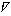 ky/
ky/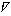 kx)i=
kx)i=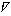 ky/hk
ky/hk
とするが、不等間隔の場合には、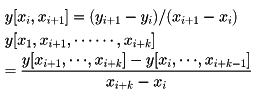
で定義される差商divided differenceというものを用いる。差分商および差商は、微分法における微分商に相当するもので、これを用いて、変化率を論じたり、補間、近似、積分などを行うことができる。
[戸川隼人]
狭義の差分法
微分方程式の近似解法の一種としての差分法がある。これは、常微分方程式および偏微分方程式の境界値問題に用いられる。原理が単純で、どんな形の方程式にもたいてい適用できることが特徴である。そのかわり、必要演算回数が多いので、コンピュータを使わないと実用的計算はできない。その原理は、微分方程式を近似する差分方程式をつくって、それを解くという方法による。近似差分方程式をつくるには、微分方程式に含まれる微分商を、その近似差分商で置き換えるのがもっとも簡単である。たとえば、微分方程式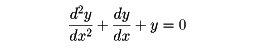
の場合、左辺第1項、第2項をそれぞれ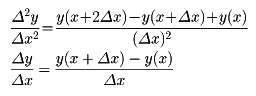
で置き換えれば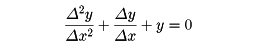
となる。ただし、このような方法がつねによい結果をもたらすとは限らないので、問題によっては慎重な考察を要する。問題とする区間を細かく等分して分点を設け、各分点において前出の差分方程式をつくり連立させ、境界条件を付加して解けば、前出の微分方程式の近似解が求められる。
[戸川隼人]
差分法の数学的根拠
関数解析学の手法により、差分法の基礎理論が研究され、多くの公式について、その収束性(分割を無限に細かくするとき厳密解に収束すること)が証明されている。
[戸川隼人]
『赤坂隆著『数値計算』(1967・コロナ社)』▽『フォーサイス、ワソー著、藤野精一訳『偏微分方程式の差分法による近似解法』上下(1968・吉岡書店)』▽『戸川隼人著『数値解析とシミュレーション』(1976・共立出版)』▽『高橋亮一・棚町芳弘著『差分法』(1991・培風館)』▽『山本哲朗著『数値解析入門』増訂版(2003・サイエンス社)』


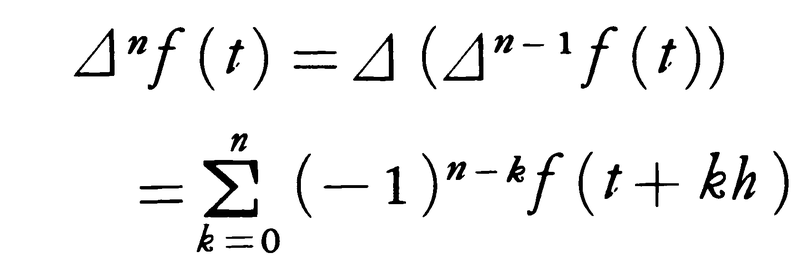
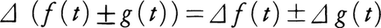
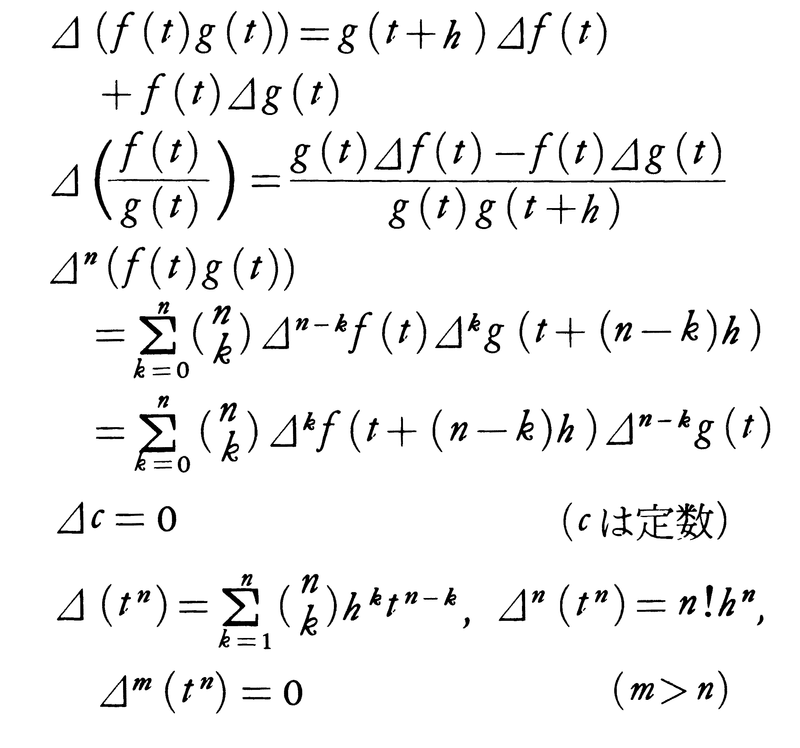
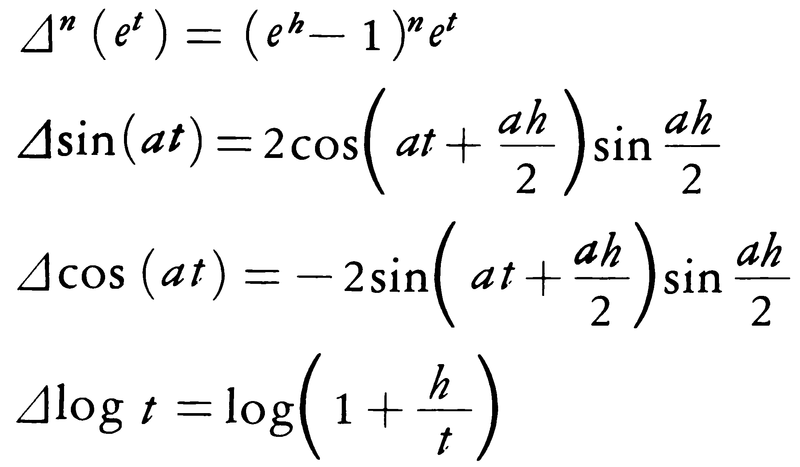
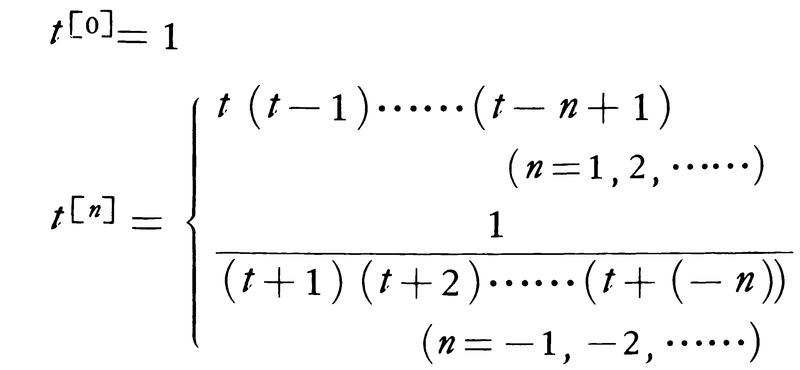
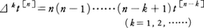 が成立する。f(t)が(a,∞)(a<0)でn+1回微分可能であるとき,t[k]を用いたf(t)の展開はニュートンの公式,
が成立する。f(t)が(a,∞)(a<0)でn+1回微分可能であるとき,t[k]を用いたf(t)の展開はニュートンの公式,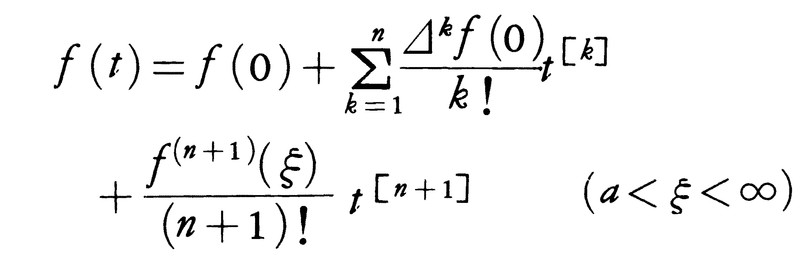
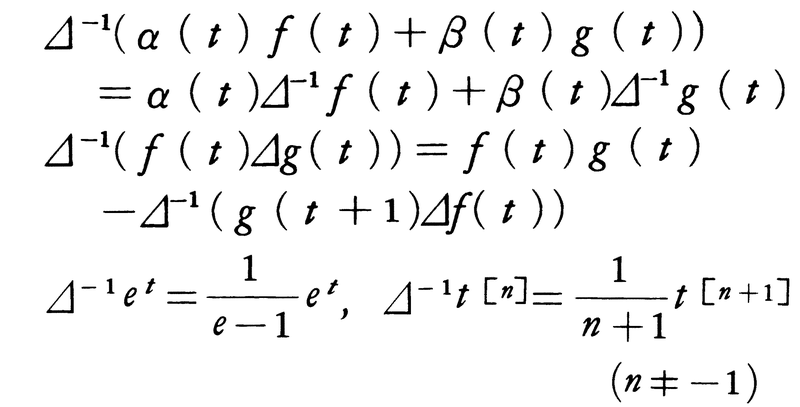
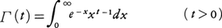 に対する基本性質Γ(t+1)=tΓ(t)(t>0)を用いると,
に対する基本性質Γ(t+1)=tΓ(t)(t>0)を用いると,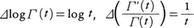 であり,それぞれに対応する和分が得られている。次に,和分の定義から得られる関係,
であり,それぞれに対応する和分が得られている。次に,和分の定義から得られる関係,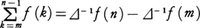 は離散型変数の級数の和を求める場合に有効である。定積分に対応するものについてはネールントE.Nörlund(1885- )その他による研究が行われている。
は離散型変数の級数の和を求める場合に有効である。定積分に対応するものについてはネールントE.Nörlund(1885- )その他による研究が行われている。