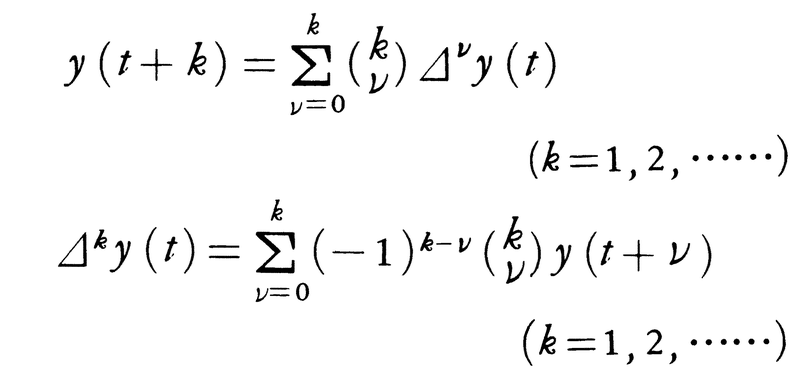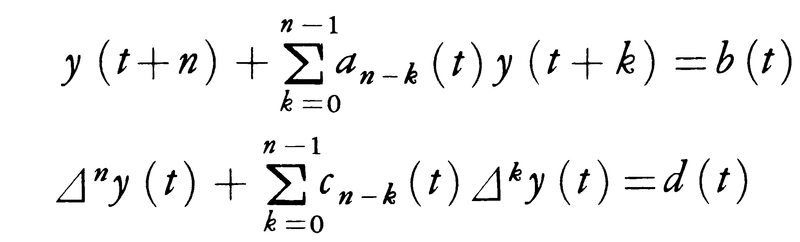差分方程式（読み）さぶんほうていしき（その他表記）difference equation

日本大百科全書(ニッポニカ)

差分方程式
さぶんほうていしき
difference equation

差分についての関係式が与えられたとき、それを満たす関数（または表関数）を求める問題を差分方程式、または定差方程式といい、式に含まれる最高階の差分の階数を、差分方程式の階数という。

［戸川隼人］

数値的解法

差分方程式に差分の定義式を代入すれば、表関数の値を未知数とする連立方程式になるから、階数と同じ個数の条件（初期条件、境界条件など）を付加すれば、数値的に解くことができる。たとえば、
　　Δy＝y,　y₁＝1
の場合、関数値の形で書けば
　　y_i＋1－y_i＝y_i
であるから、初期条件y₁＝1から出発して
　　y_i＋1＝2y_i
により順に計算すれば、次の解が得られる。

　　y₂＝2,　y₃＝4,　y₄＝8,　y₅＝16
　差分方程式の計算においては、未知数の非常に多い連立方程式を解かなければならない。しかし個々の式は比較的簡単で、一つの式に現れる未知数の個数は少ない。そのため反復法（逐次近似法）が有利であり、巧妙な計算技法がいろいろ開発されている。

［戸川隼人］

解析的方法

差分方程式は微分方程式とよく似た性質があるので、形によっては、解析的方法によって一般解を求めることができる。

［戸川隼人］

経済学への応用

経済学では、経済諸量の時間的な前後関係や変動過程を明らかにするために、しばしば差分方程式体系が利用される。以下にもっとも簡単な応用例を示す。

　いまt期の需要量、供給量、価格をそれぞれD_t、S_t、P_tと置くとき、需給関数が次の形で与えられるものとしよう。

　　D_t＝a－bP_t　（a,bは正の定数）
　　S_t＝－α＋βP_t－1　（α,βは正の定数）
すなわち、需要量は今期の価格に、供給量は前期の価格に依存するものと考えるのである。このとき、需給均等から次式が得られる。

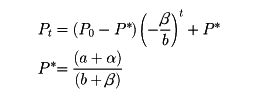
P₀はP_tの初期値、P^*は均衡値である。もしもb＞βであれば、価格は変動しながらP^*に収束し、b＜βであれば発散する。b＝βのときは、価格は一定の変動を繰り返し収束も発散もしない。これはくもの巣理論とよばれるもので、一階差分方程式の応用例である。二階差分方程式の例は、サミュエルソン型の乗数‐加速度モデルに代表される。国民所得Y_tは同期の消費C_tと投資I_tからなり、C_tは前期の所得、I_tは今期と前期の消費差に依存するものとすれば、
　　Y_t＝C_t＋I_t
　　C_t＝αY_t－1＋c
　　　（αは0＜α＜1の定数,
　　　　cは正の定数）
　　I_t＝β(C_t－C_t－1)
　　　（βは正の定数）
となり、次の二階差分方程式が導かれる。

　　Y_t＋2－α(1＋β)Y_t＋1＋αβY_t＝c
この式の解（とくに複素数解）の検討から、なぜ景気循環が発生するかという問いへの一つの説明が可能となる。

［大塚勇一郎］

『戸川隼人著『微分方程式の数値計算――有限要素法と差分法』（1973・オーム社）』▽『杉山昌平著『差分・微分方程式』復刻版（1999・共立出版）』▽『広田良吾著『差分方程式講義』（2000・サイエンス社）』

[参照項目] | くもの巣理論 | 差分法 | サミュエルソン

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

差分方程式 (さぶんほうていしき)
difference equation

差分を用いた方程式，

　F（t，y（t），⊿y（t），……，⊿ⁿy（t））＝0

あるいは，

　⊿ⁿy（t）＝G（t，y（t），⊿y（t），……，⊿ⁿ⁻¹y（t））

をn階差分方程式という。差分の定義においてh＝1の場合には関係，

を用いると，n階差分方程式は，

　H（t，y（t），y（t＋1），……，y（t＋n））＝0

あるいは，

　y（t＋n）＝K（t，y（t），y（t＋1），……，y（t＋n－1））

の形にも表される。特別な場合として，

の形の方程式をn階線形差分方程式という。微分方程式の場合と同じく，初期条件あるいは境界条件を与えることによって解の存在と一意性の問題，解の表示，解の求め方，安定性の問題などが詳細に研究されている。離散変数，区分的に定数である関数，一定期間ごとに現象をとらえる場合などを解析するためには，速度，加速度の代わりに差分を用いることが便利であり，経済現象の研究には微分方程式よりも差分方程式が多用されている。
→差分法
執筆者：杉山 昌平

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

差分方程式
さぶんほうていしき
difference equation

階差方程式，定差方程式ともいう。関数 y＝f(x) において，変数 x が Δx だけ増したとき，これに対する y の差分を Δy とする。以下第2，第3，… ，第 n 差分をそれぞれ Δ²y ，Δ³y ，… ，Δⁿy とするとき，方程式

F(x，y，Δy，Δ²y，Δ³y，…，Δⁿy)＝0

を，n 階の差分方程式という。これを満たす関数 y＝f(x) を求めることを，差分方程式を解くという。

出典　ブリタニカ国際大百科事典 小項目事典