日本大百科全書(ニッポニカ) 「待ち行列理論」の意味・わかりやすい解説
待ち行列理論
まちぎょうれつりろん
queuing theory
「待ち合わせの理論」ともいう。病院の窓口、切符売場などサービスの行われる場所で、客が多いと行列をつくってサービスを受ける順番を待つという現象がみられる。客の待つ時間が大きくなることはサービス上からみて好ましいことではない。一方、窓口や客への応対者を多くすることはむだが多くなる心配もある。客の待ち時間を少なくし、また窓口の数も効率的にするにはどのようにすればよいか。このような問題は場合場合によって多様性をもつものであるが、ある型の問題に対しては確率の考えを利用して問題を定式化し、理論的考察が可能になることがある。この理論が待ち行列理論である。
以下、この理論の初歩の部分を簡単に説明する。もっとも基本的なものとして次のようなモデルを考える。
窓口はs個あって、そこに客がやってくる。あいている窓口があれば、そこへ行ってサービスを受ける。あいた窓口がなければ行列に並んで順番を待つことになる。こうして待ち行列ができる。窓口があけば、きた順すなわち先着順にサービスを受け、終わったら窓口を立ち去る。
窓口には客が1人ずつくるものと仮定するが、次々と到着する客の到着時間間隔(次にくる客との時間間隔)を一つ一つ確率変数とみることにする。またこれらの確率変数は独立であって、すべて同一の確率分布をもつものと考える。この確率分布を到着分布という。
また窓口での1人1人の客に対するサービス時間も確率変数とみることにし、これらの確率変数は独立であって、すべて同一の確率分布をもつものと考える。この確率分布をサービス分布という。
さらに、サービス時間を表す確率変数は到着時間間隔を表す確率変数とは独立であると仮定する。
これらの仮定は多くの実際問題において満たされているものと考えられる。
ケンドールDavid Kendallは、待ち行列モデルを表すのに、Aという記号を用いた。ここでAは到着分布を、Bはサービス分布を、sは窓口の個数を表している。Aをケンドールの記号という。
次に、到着分布、サービス分布として用いられることが多い分布の例をあげる。
(1)指数分布(Mで表す) 確率分布が指数分布であるというのは、確率密度が次の形の場合である(λは正の定数)。
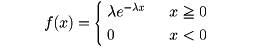
この確率分布の平均値は1/λである。到着分布が指数分布の場合には、時間区間(a,a+t)内に到着する客の人数をXとすると、Xは平均値λtのポアソン分布をもつ。この意味で到着分布が指数分布の場合、ポアソン到着とよぶことが多い。Xの分布が区間(a,a+t)の始点aに関係せず、時間間隔の長さtだけに関係していることは重要な性質である。
(2)単位分布(Dで表す) 定数である確率変数の分布が単位分布である。すなわち、cを定数としてX=cである確率が1である確率変数の分布である。到着分布が単位分布であるということは、客がいつも一定の時間間隔でやってくることである。
(3)アーラン分布(Ekで表す) 確率密度が、kを1以上の整数、λを正の定数として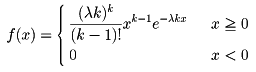
で表される分布をアーラン分布、またはk‐アーラン分布という。
この分布はkが1のとき指数分布と一致する。なお、k‐アーラン分布は、同一の指数分布をもつ独立なk個の確率変数の和の確率分布である。
このM、D、Ekの記号は、ケンドールの記号を用いる場合に使用される。
たとえば、Mは、到着分布が指数分布、サービス分布が指数分布、窓口がs個であることを意味し、Mは、到着分布が指数分布、サービス分布が単位分布、窓口が1個であることを意味している。
次にMにおいて平衡状態とよばれる特別の場合について、待ち行列の長さの平均値、待ち時間の平均値などを求めてみよう。
到着分布、サービス分布の確率密度をそれぞれf(x),g(x)とする。
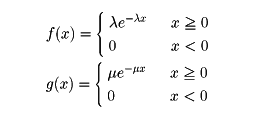
ここで、λ、μは正の定数である。
これは、単位時間に平均λ人の客がきて、サービス可能の人数が一つの窓口当り平均μ人であるということを意味している。λ>sμの場合は、全部の窓口を使っても客をさばききれないで行列が長くなる可能性が強い。λ<sμの場合は、平均的にはサービス可能の人数が客の数より多いわけである。
さて、ある時刻tにおいて、窓口でサービスを受けている客の人数と、行列をつくって順番を待っている客の人数の和がnである確率をPn(t)で表す。Pn(t)がtに無関係であるとき平衡状態という。
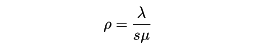
と置くと、ρ<1のとき平衡状態が存在することが知られている。平衡状態のときPn(t)をpnで表すと、pnは次式で与えられる。ここで、a=λ/μとする。
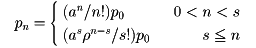
ただし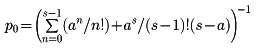
この結果を用いて、待ち行列の長さの平均値Lp、待ち行列の長さとサービス中の人数の和の平均値L、待ち時間の平均値Wq、窓口が全部ふさがっている確率πが求められる。
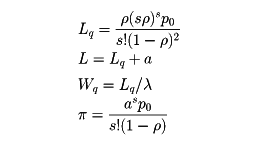
[古屋 茂]
『本間鶴千代著『待ち行列の理論』(1973・理工学社)』

