微分幾何学（読み）ビブンキカガク（英語表記）differential geometry

デジタル大辞泉

びぶん‐きかがく【微分幾何学】

微積分法を利用して、曲面・曲線の性質を研究する幾何学。

出典　小学館

精選版 日本国語大辞典

びぶん‐きかがく【微分幾何学】

〘名〙 もと、微分積分学の方法を応用して曲線や曲面の性質を研究する幾何学の一分科。ガウスによって初めて体系化された。現在では、対象も方法ももっと多様なものとなっている。

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

微分幾何学
びぶんきかがく
differential geometry

微分幾何学は、古典的な意味では、平面および空間における曲線や曲面などの性質を微分学を応用して研究する数学の一分野である。現代的には、リーマン計量、複素構造、接続などのようになんらかの構造が与えられた多様体の理論を意味する。古典的な意味の微分幾何学を確立したのはK・F・ガウスである。

　曲線や曲面、あるいは一般に多様体に関する概念や性質には、各点の十分小さい近傍(きんぼう)内の情報だけで定まるものと、全体に関連して定まるものとがある。前者を局所的（または小域的）といい、後者を大域的という。曲線や曲面の曲率は局所的概念の典型である。これに対して、凸閉曲線の幅、閉曲線の長さとその囲む面積との関係、曲面の穴の数、閉曲面上に存在する閉測地線の数などは、大域的な概念（または性質）である。局所的な性質は、微分学を主要な手段として研究されるのに対して、大域的な性質の研究には、位相幾何学やリー群論などをはじめとする他の諸分野の知識を動員する必要がある。

［荻上紘一］

平面曲線の幾何学

平面曲線を弧長sを変数としてx=x(s)と表せば、e₁=x′(s)は単位接ベクトルである。e₁を正の向きに90度回転して得られるベクトルをe₂とすれば、e₁、e₂は曲線上の各点で正規直交系をなす。このときe₁、e₂は微分方程式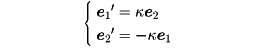

を満たす。κを曲線の曲率という。κ≡0（曲線上の各点で恒等的にゼロ）ならば直線であり、κ≡1/r（一定）ならば半径rの円である。平面曲線の局所的な性質は曲率によって完全に決まる（平面曲線の基本定理）。平面曲線に関する大域的な性質としては、四頂点定理、等周不等式、定幅曲線などが有名である。

［荻上紘一］

空間曲線の幾何学

空間曲線を弧長sを変数としてx=x(s)と表し
　e₁=x′(s),e₂=x″(s)/‖x″(s)‖,e₃=e₁×e₂
とすれば、e₁、e₂、e₃は曲線上の各点で正規直交系をなす。e₁を単位接ベクトル、e₂を単位主法線ベクトル、e₃を単位従法線ベクトルという。このときe₁、e₂、e₃は微分方程式（フレネ‐セレーの公式）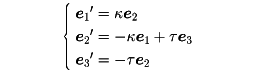

を満たす。ただし
　　κ=‖x″(s)‖,
　　τ=(1/κ²)(x′×x″)・x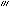
であり、κを曲率、τを捩率(れいりつ)という。曲率は曲線がその接線から離れる度合いを表し、捩率は曲線がe₁、e₂で張られる平面（接触平面という）から離れる度合いを表す。空間曲線の局所的な性質は曲率と捩率により完全に決まる（空間曲線の基本定理）。空間曲線に関する大域的な性質としてはフェンヒェルWerner Fenchel（1905―1988）やミルナーJohn Willard Milnor（1931―　）らによる全曲率∫κdsに関する不等式が有名である。

［荻上紘一］

曲面のいろいろな性質

曲面は第一基本形式と第二基本形式によって完全に決まる。第一基本形式は曲面上で長さを測る尺度を与える二次形式（すなわち二次の対称行列）で、リーマン計量の例である。第二基本形式は外からみた曲面の曲がりぐあいを表す二次形式である。

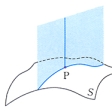
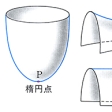
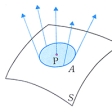
　曲面S上の点PにおいてSの法線を含む平面とSとの交線のPにおける（平面曲線としての）曲率の（平面をいろいろ変えてみたときの）最大値と最小値をSのPにおける主曲率といい、主曲率の積をガウス曲率という（図A）。ガウス曲率は曲面の「曲がりぐあい」を忠実に表す量である。Pにおけるガウス曲率が正、負、ゼロに応じてPを楕円(だえん)点、双曲点、放物点という（図B）。曲面Sの点Pに対してPにおける単位法ベクトルを対応させる写像をガウス写像という（図C）。ガウス写像はSから単位球面への写像であり、ガウス曲率はガウス写像による「面積の拡大率」に等しい。すなわちSの点Pの周りの閉曲線の囲む面積をA、ガウス写像で対応する単位球面上の閉曲線の囲む面積をA^*として、閉曲線をPに収束させたときのA^*/Aの極限がPにおけるガウス曲率に等しい。ガウス曲率が一定であるような曲面を定曲率曲面という。平面、柱面、球面などは定曲率曲面である。定曲率閉曲面は球面に限る（リープマンの定理）。主曲率の相加平均を平均曲率という。平均曲率が至る所ゼロであるような曲面を極小曲面という。極小曲面は、局所的には与えられた閉曲線を境界にもつ曲面のなかで面積が最小であるという性質をもつ。針金の輪にせっけん膜を張ってできる曲面は極小曲面である。懸垂(けんすい)線を母線とする回転面（懸垂面という）は極小曲面であるが、逆に極小曲面となる回転面は懸垂面に限る。

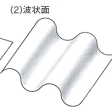
　対応する点における第一基本形式が一致するような二つの曲面は、互いに伸縮なく重ね合わせることができる（このとき二つの曲面は互いに等長であるといわれる）。対応する点における第一基本形式と第二基本形式がともに一致するような二つの曲面は、空間の運動によって重ね合わせることができる（このとき二つの曲面は合同であるといわれる）。二つの曲面は、等長であっても合同であるとは限らない。たとえば、図Dにおいて(1)と(2)は大域的に等長であるが（局所的にも）合同ではなく、(1)と(3)および(2)と(3)は、局所的に等長であるが合同ではない。曲面の局所的性質のなかでもっとも重要な結果は、「ガウス曲率が第一基本形式だけで決まる」というガウスの基本定理である。これにより互いに等長な二つの曲面は、対応する点において同じガウス曲率をもつことがわかる。しかし、この逆は成り立たない。たとえば、図Eのように長さの異なる円柱に半球の蓋(ふた)をつけた曲面を考えれば、両者の間に対応点におけるガウス曲率が一致するような1対1の対応がつけられるにもかかわらず、両者は等長ではありえない。平面と局所的に等長な曲面をとくに可展面という。曲面が可展面であるためには、そのガウス曲率が至る所ゼロであることが必要十分条件である。可展面は一径数平面族の包絡面(ほうらくめん)であり、平面、柱面、錐(すい)面、接線曲面のどれかである。

　曲面の大域的な性質のなかで有名なものとして、「互いに等長な二つの凸閉曲面は合同である」というコーン・フォッセンStefan Cohn-Vossen（1902―1936）の定理がある。このことからとくに球面は歪曲(わいきょく)不可能であることがわかる。しかし、球面から小円板を取り除いた残りは歪曲可能である。曲面に関する大域的な結果のなかでもっともすばらしい定理は、ガウス‐ボンネの定理である。すなわち、表裏が決められる閉曲面Sのガウス曲率Kとオイラー標数χ(S)の間には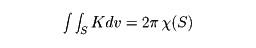

なる関係が成り立つ。オイラー標数χ(S)は、曲面Sの三角形分割に対して
　　χ(S)＝（頂点の数）－（辺の数）＋（面の数）
で定義される。ガウス‐ボンネの定理は、曲面の微分幾何学的な量（曲率）と位相幾何学的な量（オイラー標数）との間の関係を与える非常に美しい定理である。

　曲面の第一基本形式に関する性質はB・リーマンによって一般化されて、リーマン幾何学として今日に至っている。また、第二基本形式に関する性質の研究は部分多様体の幾何学に成長した。今日、微分幾何学は位相幾何学、リー群論、代数幾何学、多変数関数論、偏微分方程式論など、他の分野との関連のもとに著しい発展をしている。

［荻上紘一］

[参照項目] | リーマン幾何学

微分幾何学（ガウス曲率）〔図A〕

微分幾何学（楕円点、双曲点、放物点）〔…

微分幾何学（ガウス写像）〔図C〕

微分幾何学（等長と合同）〔図D〕

微分幾何学（長さの異なる円柱に半球の蓋…

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

微分幾何学 (びぶんきかがく)
differential geometry

現在，微分幾何学の意味するものは広い。本来はその方法論の一つとして，多様体上に定義された関数，またはそれを一般化したベクトル，テンソル場などの微分量を用いる幾何学というところからついた名称であるが，微分される対象，微分量の取扱い方，あるいは目的とする幾何学等々の差異によって，等しく微分幾何学と呼ぶものの中にもニュアンスの違いが生ずる。おおまかにいえば，それらは曲線，曲面の微分幾何学，リーマン多様体上の微分幾何学および必ずしもリーマン的とはかぎらない微分可能多様体上の微分幾何学ということになるであろう。なお，これは（実）多様体上のそれについてだけの分類であるが，複素多様体上でも同じく微分幾何学的手法は有効である。しかし，この場合，微分可能性がそのまま解析性を意味することが多いことから，より強い立場の幾何学，例えば代数幾何学などと混じり合うことが多い。

　さて，曲線，曲面の微分幾何学は，ユークリッド空間におけるユークリッド幾何学の直接の一般化であると考えてよい。すなわち，円や三角形のみを対象として，その合同分類を研究するユークリッド幾何学に代わって，ユークリッド空間における曲線や曲面の合同分類を研究するのが，曲線，曲面の微分幾何学である。例えば曲線論の場合，角度に代わって曲率，ねじれ率がその役割を果たす。これらは，曲線を表す式からの微分計算によって得られるのであるから，その名称にふさわしいといってよい。これら曲線論，曲面論を，一般の微分可能多様体の中で展開しようとするのが，より広い意味の微分幾何学の始まりである。しかしユークリッド空間の幾何学的性質のうちのどの部分を抽象化し，そのうえで曲線論，曲面論のどの部分を展開するかはさまざまであり，したがって冒頭に述べたような分化が行われた。リーマン多様体ないしその幾何学は，ユークリッド空間が，内積による距離をもつという性質を拡張し，それを保つ変換で不変な性質を研究するものである。また，ユークリッド空間に定義される平行性を拡張するものとして，接続の概念が（リーマン的でない多様体にも）導入されて，接続の幾何学として展開された。これから導かれる共変微分は，多様体上での幾何学的量であるベクトル，テンソルの高階微分を可能にするものであり，これによって，曲率，ねじれ率などのように高階の微分を必要とする概念が，多様体上でも得られることになった。また，一方では，平行ベクトルによる移動の概念も拡張され，例えば，一般のホロノミー群の概念が得られている。これらにもみられるように，ユークリッド的な性質の一部（または全部）の抽出，拡大によって幾何学を再構成し，微分量を駆使することによってその本質に迫ろうとするものが微分幾何学であるといえるようである。
執筆者：四方 義啓

出典　株式会社平凡社「改訂新版　世界大百科事典」

百科事典マイペディア

微分幾何学【びぶんきかがく】

微分・積分の方法を用い曲線・曲面の性質を研究する幾何学の一分科。19世紀初めガウスが体系化。リーマン幾何学はその重要な一部門。現代数学では，微分可能多様体の研究を意味する。
→関連項目カルタン｜幾何学｜微分｜矢野健太郎

出典　株式会社平凡社

ブリタニカ国際大百科事典 小項目事典

微分幾何学
びぶんきかがく
differential geometry

曲線，曲面，さらには空間自身の研究に微分学と積分学の手法を用いる幾何学の一分科であって，微分積分学の発見と同時に始ったということができる。しかしこれを幾何学の一分科として確立したのは C.ガウスである。 B.リーマンは，ガウスの曲面論を拡張して，一般次元の曲率をもつ空間の概念に達した。これは現在リーマン空間と呼ばれ，その幾何学はリーマン幾何学と呼ばれている。これは，C.リッチ，T.レビ＝チビタなどによって発展させられ，アインシュタインによって一般相対性理論へ応用された。リーマン幾何学は，H.ワイル，E.カルタンなどによって接続の幾何学に拡張され，現在でも盛んに研究されている。微分幾何学の最近の傾向は，図形の位相的性質も考慮に入れることと，その範囲を，概複素空間，概接触空間，およびそれらの拡張へ広めつつあることであろう。

出典　ブリタニカ国際大百科事典 小項目事典

世界大百科事典（旧版）内の微分幾何学の言及

【幾何学】より

…1930,7版)においてその完成をみた。
［微分幾何学］
　微分学は平面曲線に接線をひく方法に関するフェルマーの研究を発端として誕生したことが示すように，微分学は曲線の研究と密接な関係にあり，17世紀末葉の微積分学の成立以来，微分学の応用による曲線の研究が微分学の一部として発達した。そして，平面曲線の曲率，接触円，縮閉線，包絡線などが研究されたが，これらの研究は空間曲線に対する類似の研究へ導き，さらに曲面の曲率や測地線などの研究が18世紀にヨハン･ベルヌーイ(1667‐1748)，オイラー，J.L.ラグランジュ，モンジュらによって微積分学の応用として行われた。…

※「微分幾何学」について言及している用語解説の一部を掲載しています。

出典｜株式会社平凡社「世界大百科事典（旧版）」