対数（読み）タイスウ

デジタル大辞泉

たい‐すう【対数】

x＝a^y（a≠1, a＞0, x＞0）という関係があるとき、yをaを底ていとするxの対数といい、y＝log_axと表す。xを対数yの真数という。ロガリズム（logarithm）。

出典　小学館

精選版 日本国語大辞典

たい‐すう【対数】

1. 〘 名詞 〙 実数の一つ。ａが１以外の正数のとき、正数Ｎ、実数ｂの間に N=a^b という関係があるならば、ｂのことをａを底(てい)とするＮの対数といい、b=log_aN で表わす。正数の乗法、除法は、その対数の加法、減法に対応する。〔工学字彙（1886）〕

出典　精選版 日本国語大辞典

日本大百科全書(ニッポニカ)

対数
たいすう

aを定数とするとき、数xに対し、
　　x=a^y……(1)
を満たす数yを、（aを底(てい)とする）xの対数といい、
　　y=log_ax……(2)
と書く（logは、対数を意味する英語logarithmを略した記号）。すなわち、(1)と(2)は同値である。このとき、xをyの真数という。たとえば、8=2³,0.01=10^-2であるから、それぞれ3=log₂8,-2=log₁₀0.01である。y=log_axは指数関数y=a^xの逆関数であり、aを1でない正の数とすれば、どんな正の数xに対しても、aを底とする対数yが一つだけ定まる。以下、底についてはa＞0,a≠1、真数については正とする。1=a⁰,a=a¹であるから、つねにlog_a1=0,log_aa=1が成り立つ。また、α=log_aA,β=log_aBとすればA=a^α,B=a^βで、指数法則によりAB=a^α・a^β=a^α+βすなわちlog_aAB=α+β、したがって
　　log_aAB
　　 =log_aA+log_aB……(3)
が成り立つ。同様にして
　　log_a(A/B)
　　 =log_aA-log_aB……(4)
pを任意の実数としてlog_aA^p=plog_aAで、とくに、nを自然数として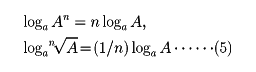

が導かれる。これらの公式から、二つの正の数A、Bの積、商がそれぞれの対数の和、差を利用して求められる。また、正の数Aのn乗、n乗根がそれぞれlog_aAのn倍、n分の1を利用して求められる。なお、異なる底をもつ対数の間には次の関係がある。

　　log_aA=log_bA/log_ba……(6)
このような計算を対数計算という。

　10を底とする対数を常用対数という。常用対数については次のような計算ができる。

　　log₁₀2000
　　　　　　=log₁₀(2×10³)
　　　　　　=3+log₁₀2
　　log₁₀0.002
　　　　　　=log₁₀(2×10^-3)
　　　　　　=-3+log₁₀2
同じようにして、log₁₀2の値から、nを整数として2×10ⁿの形の数の対数の値を求めることができる。一般に1≦x＜10の範囲にあるxについて、log₁₀xの値が与えられればx×10ⁿの形の数の対数の値を求めることができる。この範囲にある数の常用対数の値の表が対数表である。たとえば対数表からlog₁₀3.14=0.4969が得られる。よって
　　log₁₀3140=3+log₁₀3.14
　　　　　　　=3.4969
　　log₁₀0.0314=-2+log₁₀3.14
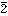　　　　　　　=.4969
これらの最後の形をみればわかるように、対数表から対数の値を求めるときは、3、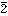のような整数部分と、4969のような小数部分に分けて扱うと都合がよい。前者を指標、後者を仮数とよぶ。指標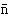は-nと同じ意味である。

　対数を用いる計算例として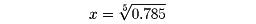

の値を求めてみよう。

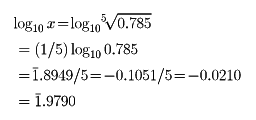
よって　x=0.9528
前述の最後でlog₁₀xの値からxを求めるのに対数表を逆に用いてもよいが、このために、対数の値に真数の値を対応させた逆対数表、すなわちy=10^x(0≦x＜1)の値の表もつくられている。

　長い間、対数計算は数値計算の労力を減らすのに役だってきたが、近年、コンピュータの発達によって、利用されることが少なくなった。数直線で、座標log₁₀xの点にxと目盛ったものを対数目盛りとよぶ。この目盛りを用いた方眼紙を対数方眼紙といい、実験式を求めたりするのに利用される。常用対数のほかに、eを底とする対数も広く用いられている。

［植竹恒男］

[参照項目] | 逆関数 | 指数関数 | 自然対数

出典　小学館　日本大百科全書(ニッポニカ)

改訂新版　世界大百科事典

対数 (たいすう)
logarithm

aを1でない正の数，xを任意の正の数とすると，a^u＝xとなる実数uが定まる。このuを〈aを底（てい）とするxの対数〉といい，u＝log_axと書く。またこのとき，xをuの真数という。aを定めて，xの値に対するlog_axの値を与える数値表を対数表という。対数の基本的な性質としては，

　log_a1＝0，log_aa＝1　……（1）　

　log_axy＝log_ax＋log_ay　……（2）　

　log_a（x/y）＝log_ax－log_ay　……（3）　

　log_ax^p＝plog_ax（pは任意の実数）　……（4）　

　対数表によってx，yの対数log_ax，log_ayを求め，和log_ax＋log_ay＝log_axyを計算して，対数表を逆に引くことによりlog_axyの真数xyを求めることができるから，真数の乗法が対数表によって対数の加法で置き換えられる。同様に，（3）により除法が減法で置き換えられ，（4）により累乗，または累乗根を求める計算がそれぞれ乗法，除法で置き換えられる。

　対数が史上に登場したのはこのような実用上の目的による。ビュルギJobst Bürgi（1552-1632）は1603-11年の間に対数表を作り，20年にそれを刊行した。それとは無関係に，J.ネーピアも1617年に対数表を公表し，これが対数の初めといわれる。

　ふつうの記数法は十進法によるので，実用上の計算には10を底とする対数を用いるのが便利である。この対数を常用対数common logarithmと呼び，初等数学では底10を省略してlogxと書く。このとき公式（1）によりlog10＝1となる。x≧1であってxの整数部分がn＋1桁（n≧0）の数ならば，x＝10ⁿx′，1≦x′＜10と書けるから，logx＝n＋logx′，0≦logx′＜1となる。また，0＜x＜1であって，xの小数第n位に初めて0でない数字が現れるならば，x＝10ⁿ′x′，n′＝－n，1≦x′＜10と書けるから，logx＝n′＋logx′，0≦logx′＜1となる。上記のn（x≧1の場合），またはn′（0＜x＜1の場合）を対数logxの指標といい，logx′を仮数という。すなわち，1≦x′＜10なるx′に対する常用対数の表から，その対数（すなわち仮数）を求めれば，それにxの桁数から定まる整数n，またはn′（すなわち指標）を加えることにより，xの対数が得られる。常用対数表はこの原理によって作られ，1794年にベガG.Vegaによって完全なものとされた。

　しかし，数学の理論においては，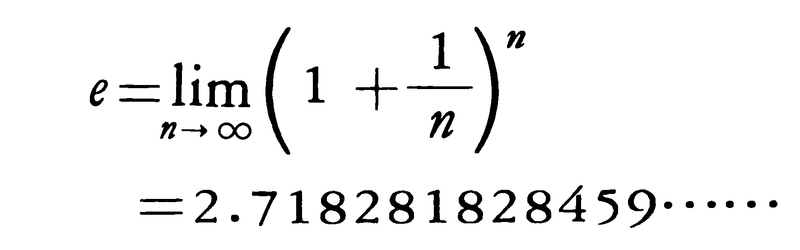

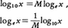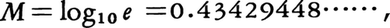
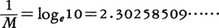を底とする対数log_exが用いられる。この対数を自然対数natural logarithmと呼んで，これを単にlogxで表すが，lnxとも書かれる。自然対数と常用対数との関係は，ただし，である。
→指数関数　→指数法則　→対数関数
執筆者：伊藤 清三

出典　株式会社平凡社「改訂新版　世界大百科事典」

ブリタニカ国際大百科事典 小項目事典

対数
たいすう
logarithm

a が1とは異なる正の数であって，x ，y の間に，x＝a^y なる関係があるとき，指数 y を，a を底とする x の対数といい，y＝ log _ax と書き表わす。ここで，x は対数 y の真数と呼ばれる。対数 y は，真数 x を求めるために底 a を累乗すべき指数を意味する。任意の正の数 a ( a≠1 ) を底とする正の数 x の対数は，常に存在する。負であるような x の対数は実数の範囲では存在しない。 a を底とする x の対数が与えられたとき，他の数 b を底とする x の対数 y' は，
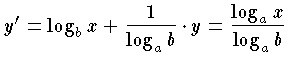によって求めることができる。上の公式のなかの 1/ log _ab を，対数の換算モジュラスという。底 a が 10の場合の対数を常用対数またはブリッグスの対数といい，普通の実用計算に用いられる。 x の常用対数 y は，一般に底 10を省略して，単に log x (あるいは lgx ) と書く。底が e＝2.71828 …の場合の対数を，自然対数またはネーピアの対数といい，理論的な面や，科学，工学などで用いられ， log _ex (あるいは ln x ) と書く。この自然対数は，双曲線対数と呼ばれることもある。自然対数から常用対数への換算モジュラスは 1/ log _e10＝0.43429 …，常用対数から自然対数への換算モジュラスは 1/ log ₁₀e＝2.30259… のように示される。自然対数と常用対数のほかに，情報理論や論理では， log ₂x (あるいは lbx ) もよく使われる。

出典　ブリタニカ国際大百科事典 小項目事典

百科事典マイペディア

対数【たいすう】

aを１でない正数とするとき，正数xに対しx＝a(y/)となる実数yがただ一つ存在する。yを，aを底とするxの対数といい，y＝log(/a)xと書く。xをyの真数という。log(/a)（xx′）＝log(/a)x＋log(/a)x′，log(/a)（x(b/)）＝blog(/a)xの関係が成り立つので，乗除の計算が加減の計算に，べきやべき根の計算は乗除の計算に変えられる。数の計算には10を底とする常用対数，理論的な問題にはe（近似値2.71828……）を底とする自然対数が用いられる。log(/a)xをxの関数とみるときこれを対数関数といい，指数関数の逆関数である。→対数目盛
→関連項目計算尺｜指数｜ログ

出典　株式会社平凡社