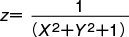極射影（読み）きょくしゃえい

ブリタニカ国際大百科事典 小項目事典

極射影
きょくしゃえい
stereographic projection

直交座標系 O-xyz において，中心 Cの座標が（0，0，1/2），半径 1/2 の球 x²＋y²＋z²＝z の上の任意の点 P（x，y，z）と，球上の定点 N（0，0，1）とを通る直線が，原点 Oで球と接する平面π（πの方程式は z＝0）と交わる点を Q（X，Y，0）とすると，Pと Qの間には
，，
という対応関係が成り立つ。この対応 P→Q は，点 Nを除いた球面上から平面πへの一対一写像とみることができる。この写像を極射影という。

出典　ブリタニカ国際大百科事典 小項目事典

日本大百科全書(ニッポニカ)

極射影
きょくしゃえい

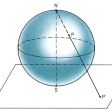
平面上に球面を置き、球面の南極をS、北極をNとする。球面上のN以外の点Pに対して、N、Pを通る直線と平面との交点をP′として点Pに点P′を対応させれば、1点Nを除いた球面上の点全体の集合と平面上の点全体の集合との間に一対一対応ができる。この対応を極Nに関する極射影という。とくに球面上の点Sに対応する平面上の点はS自身である。球面上にある2曲線c₁、c₂の極射影による像をc₁′、c₂′とすると、c₁、c₂のなす角（交点でそれぞれの接線のつくる角）はc₁′、c₂′のなす角に等しい（等角写像、共形対応）。球面上にあるNを通らない円は極射影によって平面上の円に対応する（円円対応）。また、平面上でどの方向のどんな遠方に行ってもN′に無限に近づくという架空の1点N′を考え、それを無限遠点とよぶ。極射影によるNの像をN′と約束すれば、平面にN'を付加した集合は球面と位相同形（一対一両連続対応があること）であることがわかる。

［立花俊一］

[参照項目] | 射影平面

極射影（極Nに関する極射影）

出典　小学館　日本大百科全書(ニッポニカ)